Задачи на нахождение площади куба

Обновлено: 10.01.2025

Задача 2. Площадь большого круга шара равна Найдите площадь поверхности шара.

Радиус большого круга – радиус шара. Поэтому

Площадь поверхности шара вычисляется по формуле

Задача 3. Площадь поверхности шара равна Найдите площадь большого круга шара.

Радиус большого круга – радиус шара.

Площадь поверхности шара:

Стало быть и площадь большого круга () равна

Задача 4. Во сколько раз увеличится площадь поверхности шара, если радиус шара увеличить в раз?

Площади поверхностей подобных тел находятся в отношении где – коэффициент подобия.

Поэтому площади поверхностей будут отличаться в раз.

Задача 5. Во сколько раз увеличится объем шара, если его радиус увеличить в пять раз?

Объемы подобных тел находятся в отношении где – коэффициент подобия.

Поэтому объемы будут отличаться в то есть в раз.

Задача 6. Объем первого шара в раз больше объема второго. Во сколько раз площадь поверхности первого шара больше площади поверхности второго?

Объемы подобных тел находятся в отношении где – коэффициент подобия. А так как то

Площади поверхностей подобных тел находятся в отношении где – коэффициент подобия.

Поэтому площади поверхностей будут отличаться в раз.

Задача 7. Радиусы двух шаров равны и Найдите радиус шара, площадь поверхности которого равна сумме площадей их поверхностей.

Площадь поверхности шара с радиусом есть

Сумма площадей поверхностей шаров есть

Тогда, если радиус третьего шара – это , то

Задача 8. Радиусы трех шаров равны , и Найдите радиус шара, объем которого равен сумме их объемов.

Объем шара радиуса есть

Пусть радиус четвертого шара – . Тогда

Вы можете пройти тест

Автор: egeMax | комментариев 7

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Похожие статьи на сайте.

05. Цилиндр.
05. Куб. Параллелепипед
05. Составные многогранники. Углы и расстояния
05. Призма
05. Конус
05. Комбинации тел

Мне кажется стоит сделать так же, как вы делали в предыдущих статьях: в каждой статье оставить ссылки на другие фигуры

Формулы для куба

Примем следующие обозначения, которые будут использоваться далее:

Диагональ

Длина диагонали куба равняется длине его ребра, умноженной на квадратный корень из трех.

Диагональ грани

Диагональ грани куба равна его ребру, умноженному на квадратный корень из двух.

Площадь полной поверхности

Площадь полной поверхности куба равняется шести площадям его грани. В формуле может использоваться длина ребра или диагонали.

Периметр ребер

Периметр куба равен длине его ребра, умноженной на 12. Также может рассчитываться через диагональ.

Формула вычисления площади куба

1. Через длину ребра

Площадь (S) поверхности куба равна произведению числа 6 на длину его ребра в квадрате.

S = 6 ⋅ a 2

Данная формула получена следующим образом:

2. Через длину диагонали грани

Сторона любой грани куба (ребро) может быть рассчитана через длину ее диагонали по формуле: a=d/√ 2 .

Это значит, что вычислить площадь поверхности фигуры можно так:

S = 6 ⋅ (d/√ 2 ) 2

Задачи на нахождение площади куба

Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 40 и высота равна 15.

Площадь поверхности складывается из площади основания и площади четырех боковых граней: Высоту боковой грани найдем по теореме Пифагора: Тогда площадь поверхности пирамиды:

Ответ: 3600 Источник: Пробный экзамен Санкт-Петербург 11.04.2017. Вариант 2. Задание 13 № 25549

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 4, 3 и двух площадей прямоугольников со сторонами 2, 1:

Задание 13 № 25569

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 3, 3, 4 и двух площадей квадратов со стороной 2:

Гость 22.11.2015 09:41

Там же "квадраты" со сторонами 2 и 3.

Ирина Сафиулина

Мы вычитаем, только боковые грани из большого прямоугольного параллелепипеда - это как раз квадраты со сторонами 2 и 2.

Задание 13 № 25589

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна разности площади поверхности прямоугольного параллелепипеда с ребрами 2, 3, 5 и площади двух прямоугольников со сторонами 1, 2:

Задание 13 № 25645

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Задание 13 № 25649

Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 4, 1 и двух прямоугольников со сторонами 1 и 2, уменьшенной на площадь двух квадратов со стороной 2:

Задания Д13 № 27075

Из единичного куба вырезана правильная четырехугольная призма со стороной основания 0,5 и боковым ребром 1. Найдите площадь поверхности оставшейся части куба.

Задание 13 № 507961

Деталь имеет форму изображённого на рисунке многогранника (все двугранные углы прямые). Цифры на рисунке обозначают длины рёбер в сантиметрах. Найдите площадь поверхности этой детали. Ответ дайте в квадратных сантиметрах.

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 3, 5, 7 и двух прямоугольников со сторонами 1 и 5, уменьшенной на площадь двух прямоугольников со сторонами 1 и 3:

Задание 13 № 508045

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 4, 3, 6 и двух прямоугольников со сторонами 2 и 3, уменьшенной на площадь двух прямоугольников со сторонами 3 и 2:

Задание 13 № 510029

Площадь поверхности заданного многогранника равна сумме площадей поверхности прямоугольного параллелепипеда с ребрами 5, 5, 6 и двух прямоугольников со сторонами 2 и 5, уменьшенной на площадь двух прямоугольников со сторонами 2 и 3:

Как сделать процесс подготовки к аттестационному испытанию более легким и эффективным?

Наш образовательный портал предлагает выстроить занятия по-новому. Переходя от простого к сложному, выпускники смогут определить непонятные для себя темы и улучшить собственные знания.

Весь базовый материал по теме «Вычисление площадей и объемов фигур» собран в разделе «Теоретическая справка». Освежив в памяти эту информацию, учащиеся смогут попрактиковаться в решении задач. Большая подборка упражнений как простого, так и экспертного уровня представлена в разделе «Каталог». База заданий регулярно дополняется.

Решать задачи на вычисление объемов фигур или на построение сечения геометрических фигур школьники могут в режиме онлайн. Функционал образовательного сайта «Школково» позволяет сохранять упражнения в разделе «Избранное». Благодаря этому учащиеся смогут вернуться к задаче необходимое количество раз и обсудить ход ее решения со школьным учителем или репетитором.

Задачи по теме «Куб»

Куб – это прямоугольный параллелепипед, все грани которого – равные квадраты.

\(\blacktriangleright\) для объема куба верна следующая формула (где \(a\) – ребро куба): \[<\Large>\] \(\blacktriangleright\) диагональ куба \(<\Large=3a^2>>\)
\(\blacktriangleright\) площадь поверхности куба равна сумме площадей шести одинаковых квадратов, т.е. \(<\Large>=6a^2>>\)

Уровень задания: Сложнее ЕГЭ

Дан куб \(ABCDA_1B_1C_1D_1\) . Точка \(B_2\) лежит на продолжении ребра \(BB_1\) за точку \(B_1\) , \(BB_2 = 2\cdot BB_1\) . Во сколько раз объем куба отличается от объема пирамиды \(B_2ABCD\) ?

Отрезок \(BB_2\) является высотой пирамиды. Если сторону куба обозначить за \(x\) , то \(BB_2 = 2x\) \(\Rightarrow\) \[\displaystyle V_> = \frac\cdot BB_2 \cdot S_ = \frac\cdot 2x \cdot x^2 = \frac\cdot x^3,\,\,\,\, V_> = x^3.\] Теперь найдем искомую величину: \[\displaystyle \frac>> = \frac<\frac\cdot x^3> = 1,5.\]

Уровень задания: Сложнее ЕГЭ

\(ABCDA_1B_1C_1D_1\) – куб с длиной ребра равной \(\sqrt[4]\) . Точка \(M\) лежит на ребре \(DD_1\) так, что \(MD_1 = 3MD\) . Найдите площадь сечения куба, проведённого через точку \(M\) и ребро \(AB\) .

Пусть \(N\) – точка на \(CC_1\) , такая что \(NC_1 = 3NC\) , тогда \(MN\parallel CD\parallel AB\) , следовательно, сечение, проходящее через точку \(M\) и ребро \(AB\) – четырёхугольник \(AMNB\) , причём \((AA_1D_1D) \bot MN\) , следовательно, \(AM \bot MN\) . Аналогично \(MN\bot BN\bot AB\) , то есть \(AMNB\) – прямоугольник. \[S_ = AM\cdot MN = AM\cdot \sqrt[4].\] Найдём \(AM\) по теореме Пифагора: \[AM = \sqrt = \sqrt = \sqrt<\dfracAD^2> = \dfrac<\sqrt>AD = \dfrac>.\] Тогда \(S_ = \dfrac> \cdot \sqrt[4] = \dfrac = 4,25\) .

Уровень задания: Сложнее ЕГЭ

В кубе \(ABCDA_1B_1C_1D_1\) точки \(A_2\) и \(B_2\) – середины соответственно сторон \(AA_1\) и \(BB_1\) . Найдите площадь поверхности фигуры \(ABCDA_2B_2C_1D_1\) , если ребро куба равно \(\sqrt\) .

Площадь поверхности фигуры \(ABCDA_2B_2C_1D_1\) состоит из суммы следующих площадей: \[S_> = S_ + S_ + S_ + S_ + S_ + S_.\] Обозначим ребро куба за \(2x\) , тогда \(AA_2 = BB_2 = x\) . \(AA_2D_1D\) и \(BB_2C_1C\) – равные прямоугольные трапеции, площадь которых равна \[\displaystyle S_ = S_ = \frac\cdot(AA_2 + DD_1)\cdot AD = \frac<(x + 2x)\cdot2x> = 3x^2.\] Также найдем площади остальных граней: \(S_ = 4x^2\) , \(S_ = 2x^2\) , \(S_ = 4x^2\) ; для того чтобы найти площадь грани \(A_2B_2C_1D_1\) нам понадобится сначала найти сторону \(A_2D_1\) . Найдем ее, используя теорему Пифагора в треугольнике \(\triangle A_2A_1D_1\) : \[A_2D_1^2 = A_2A_1^2 + A_1D_1^2 = x^2 + 4x^2 = 5x^2\] \(\Rightarrow\) \(A_2D_1 = \sqrt5x\) . Тогда \(S_ = A_2B_2\cdot A_2D_1 = 2\sqrt5x^2\) . Теперь сложим все площади граней искомой фигуры: \[S_> = 3x^2 + 3x^2 + 4x^2 + 2x^2 + 4x^2 + 2\sqrt5x^2 = (16 + 2\sqrt5)\cdot x^2.\] По условию задачи имеем: \(2x = \sqrt = 2\cdot\sqrt\) \(\Rightarrow\) \(x = \sqrt\) . Подставим в формулу площади и получим окончательный результат: \[S_> = (16 + 2\sqrt5)\cdot\left(\sqrt\right)^2 = 2\cdot(8 + \sqrt5)\cdot(8 - \sqrt5) = 2\cdot59 = 118.\]

Уровень задания: Сложнее ЕГЭ

Анатолий грабит банк. Слитки золота имеют форму прямоугольных параллелепипедов с измерениями \(4\times 4\times 2\) . Сумка, которая есть у Анатолия, имеет форму куба с ребром длины \(6\) . Анатолию нужно уложить как можно больше слитков в сумку так, чтобы она закрылась и с ней можно было выйти, не привлекая к ней внимания. Сколько слитков сможет вынести Анатолий, если будет действовать разумно?

Сначала заметим, что ответ не изменится, если уменьшить масштаб в два раза по каждому направлению. При этом сумка станет кубом с ребром \(3\) , а слитки золота станут прямоугольными параллелепипедами с измерениями \(2\times 2\times 1\) .

Оценим возможное количество слитков сверху: так как объём сумки равен \(3^3 = 27\) , а объём слитка равен \(2\cdot 2\cdot 1 = 4\) , то более \(6\) слитков в сумку не войдут. Но могут ли войти в неё 6?

Назовём слиток горизонтальным, если две его грани параллельны дну сумки так, что его высота равна 1. В противном случае назовём слиток вертикальным. Мысленно “расслоим” \(\ \) сумку на 3 одинаковых горизонтальных слоя.

Каждый вертикальный слиток занимает в среднем слое по 2 соседних кубика с ребром 1. Средний слой состоит из 9 таких кубиков, следовательно, вертикальных слитков в сумку входит не более 4. При этом горизонтальных слитков в сумку входит не более 3 (в каждый слой входит не более одного горизонтального слитка).

В случае, когда горизонтальных слитков ровно 3, получим, что в среднем слое 4 кубика из 9 заняты горизонтальным слитком, то есть в среднем слое остаётся \(9 - 4 = 5\) кубиков, но каждый вертикальный слиток должен занимать в среднем слое по 2 кубика, тогда получаем, что вертикальных слитков при этом не более 2 и всего слитков при трёх горизонтальных \(\leq 2 + 3 = 5\) .

Таким образом, последний шанс Анатолия унести 6 слитков – это 4 вертикальных слитка и 2 горизонтальных. Возможно ли это? Понятно, что для этого необходимо, чтобы горизонтальные слитки лежали в нижнем и верхнем слоях, но верхний слиток не должен “полностью нависать” \(\ \) над нижним. Тогда остаётся всего 2 принципиально различных способа уложить горизонтальные слитки в верхнем и нижнем слоях относительно друг друга.

При этом один из них позволяет уложить 6 слитков. Чтобы наглядно проиллюстрировать его сначала поместим в сумку только вертикальные слитки и покажем вид сверху:

здесь голубым отмечены все те вертикальные слитки, которые стоят на дне сумки. Тогда на дно можно подложить ещё 1 горизонтальный слиток под те вертикальные, которые не стоят на дне сумки. Аналогично, в верхний слой можно подложить 1 горизонтальный слиток.

Свойства куба

Свойство 1

Как следует из определения, все ребра и грани куба равны. Также противоположные грани фигуры попарно параллельны, т.е.:

Свойство 2

Диагонали куба (их всего 4) равны и в точке пересечения делятся пополам.

Свойство 3

Все двугранные углы куба (углы между двумя гранями) равны 90°, т.е. являются прямыми.

Например, на рисунке выше угол между гранями ABCD и AA₁B₁B является прямым.

Вычисление объемов фигур

Радиус первого шара в \(5\) раз больше радиуса второго шара. Во сколько раз площадь поверхности второго шара меньше площади поверхности первого шара?

Площадь поверхности шара радиуса \(R\) ищется по формуле \(S=4\pi R^2\) . Следовательно, площадь поверхности первого шара относится к площади поверхности второго шара как \[\dfrac=\dfrac<4\pi \, R_1^2><4\pi \, R_2^2>\] Так как радиус первого шара больше радиуса второго шара в 5 раз, то \(R_1=5R_2\) . Следовательно, \[\dfrac=\dfrac=25.\] Следовательно, площадь поверхности первого шара в 25 раз больше площади поверхности второго, значит, площадь поверхности второго в 25 раз меньше.

Уровень задания: Равен ЕГЭ

Даны два конуса. Радиус второго конуса в \(3\) раза больше радиуса первого конуса, а высота второго конуса в \(6\) раз меньше высоты первого конуса. Найдите объем первого конуса, если объем второго конуса равен \(18\) .

Объем конуса с высотой \(h\) и радиусом основания \(R\) вычисляется по формуле \(V=\frac13\pi R^2h\) . Следовательно, объем первого конуса относится к объему второго конуса как \[\dfrac=\dfrac= \dfrac<\frac13\pi \,R_1^2\,h_1>=\left(\dfrac\right)^2\cdot \dfrac\] Так как радиус второго в 3 раза больше радиуса первого, то \(R_2=3R_1\) . Так как высота второго в 6 раз меньше высоты первого, то \(h_1=6h_2\) . Следовательно, \[\dfrac=\left(\dfrac\right)^2\cdot \dfrac= \dfrac19\cdot 6=\dfrac23 \quad\Rightarrow\quad V_1=\dfrac23\cdot 18=12.\]

Уровень задания: Равен ЕГЭ

Даны два конуса: \(K_1\) и \(K_2\) . Площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \(4:1\) . Известно, что радиус \(K_1\) в 4 раза больше образующей \(K_1\) и в 2 раза больше радиуса \(K_2\) . Найдите отношение образующей \(K_2\) к образующей \(K_1\) .

Площадь полной поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi R (R+l)\) . Тогда площадь полной поверхности \(K_1\) относится к площади полной поверхности \(K_2\) как \[\dfrac41=\dfrac<\pi \,R_1\cdot (R_1+l_1)><\pi \, R_2\cdot (R_2+l_2)>\] Из условия следует, что \(R_1=4l_1\) , \(R_2=\frac12R_1=2l_1\) , следовательно, \[\dfrac41=\dfrac \quad\Rightarrow\quad \dfrac=\dfrac12=0,5\]

Уровень задания: Равен ЕГЭ

Во сколько раз радиус первого шара больше радиуса второго шара, если объем первого шара в \(343\) раза больше объема второго шара?

Объем шара радиуса \(R\) ищется по формуле \(V=\dfrac43 \pi R^3\) . Следовательно, объем первого шара относится к объему второго как \[\dfrac1=\dfrac=\dfrac= \left(\dfrac\right)^3 \quad\Rightarrow\quad \dfrac=\sqrt[3]=7.\] Следовательно, радиус первого шара в 7 раз больше радиуса второго шара.

Уровень задания: Равен ЕГЭ

Объем первого прямоугольного параллелепипеда равен 105. Найдите объем второго прямоугольного параллелепипеда, если известно, что высота первого параллелепипеда в 7 раз больше высоты второго, ширина второго в 2 раза больше ширины первого, а длина первого в 3 раза больше длины второго.

Пусть буквы \(a\) , \(b\) и \(c\) обозначают высоту, ширину и длину соответственно. Объем прямоугольного параллелепипеда ищется по формуле \(V=abc\) . Следовательно, объем первого параллелепипеда относится к объему второго как \[\dfrac=\dfrac=\dfrac\] Из условия следует, что \(a_1=7a_2\) , \(b_2=2b_1\) , \(c_1=3c_2\) . Тогда \[\dfrac=\dfrac= \dfrac2 \quad\Rightarrow\quad V_2=\dfrac=10.\]

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности первого цилиндра равна \(16\) . Найдите площадь боковой поверхности второго цилиндра, если его радиус в 4 раза больше радиуса первого, а высота в 5 раз меньше высоты первого цилиндра.

Площадь боковой поверхности цилиндра с высотой \(H\) и радиусом основания \(R\) ищется по формуле \(S=2\pi RH\) . Тогда площадь бок. поверхности первого цилиндра относится к площади бок. поверхности второго как \[\dfrac=\dfrac=\dfrac<2\pi \,R_1\,H_1><2\pi \,R_2\,H_2>= \dfrac\cdot \dfrac\] Из условия следует, что \(R_2=4R_1\) , \(H_1=5H_2\) , значит, \[\dfrac=\dfrac\cdot \dfrac= \dfrac14\cdot 5=\dfrac54\] Следовательно, \[S_2=\dfrac5=12,8.\]

Уровень задания: Равен ЕГЭ

Площадь боковой поверхности первого конуса относится к площади боковой поверхности второго конуса как \(3:7\) . Найдите отношение образующей первого конуса к образующей второго конуса, если радиус первого конуса относится к радиусу второго как \(15:7\) .

Площадь боковой поверхности конуса с образующей \(l\) и радиусом основания \(R\) ищется по формуле \(S=\pi Rl\) . Тогда площадь бок. поверхности первого конуса относится к площади бок. поверхности второго как \[\dfrac 37=\dfrac=\dfrac<\pi R_1\,l_1><\pi R_2\,l_2>\] Так как радиус первого конуса относится к радиусу второго как \(15:7\) , то есть \(\frac=\frac7\) , то \[\dfrac37=\dfrac 7\cdot \dfrac \quad\Rightarrow\quad \dfrac=\dfrac37\cdot \dfrac7=\dfrac15=0,2.\]

Мои задачи Добавить папку Мои задачи

Во время подготовки к сдаче ЕГЭ по математике повторение базовых формул из школьного курса геометрии в пространстве (стереометрии), в том числе и для вычисления объемов фигур, является одним из основных этапов. И хотя на изучение этого раздела отводится достаточно большое количество времени в рамках учебной программы, многим выпускникам требуется освежить в памяти основной материал.

Понимая, как осуществляется вычисление площадей объемных фигур, учащиеся значительно повышают свои шансы на получение достойных баллов по итогам сдачи ЕГЭ.

Определение куба

Куб – это правильный многогранник, все грани которого являются квадратами.

Примечание: куб является частным случаем параллелепипеда или призмы.

Задачи по теме «Прямоугольный параллелепипед»

\(\blacktriangleright\) Прямоугольный параллелепипед – это параллелепипед, все грани которого являются прямоугольниками.
Другими словами, это прямая призма, основания которой – прямоугольники.
(эти определения эквивалентны).

1) противоположные грани равны между собой;

2) боковые ребра перпендикулярны основаниям, то есть являются высотами;

3) как следствие, формула для объема принимает вид: \(<\Large>\) , где \(a,\ b,\ c\) – три различных боковых ребра.

\(\blacktriangleright\) Диагональ прямоугольного параллелепипеда – это отрезок, соединяющий две противоположные (не лежащие в одной грани) вершины.

1) Все диагонали равны, пересекаются в одной точке и делятся ею пополам;

2) Диагональ \(d\) можно найти по формуле: \(<\Large=a^2+b^2+c^2>>\) .

Уровень задания: Легче ЕГЭ

Дан прямоугольный параллелепипед, стороны основания которого равны \(4\) и \(5\) , а боковое ребро равно \(3\) . Найдите наибольшую площадь его грани.

Заметим, что все варианты для площадей его граней – это всевозможные попарные произведения чисел \(3,4,5\) , то есть \(3\cdot 4\) , \(4\cdot 5\) или \(3\cdot 5\) . Среди этих произведений наибольшим является \(4\cdot 5=20\) .

Уровень задания: Легче ЕГЭ

Даны два прямоугольных параллелепипеда: ребра одного равны \(185\) , \(185\) и \(37\) ; а ребра другого равны \(185, 37\) и \(37\) . Во сколько раз объем первого параллелепипеда больше объема второго параллелепипеда?

Уровень задания: Легче ЕГЭ

Даны два прямоугольных параллелепипеда: ребра одного равны \(a, b\) и \(b\) , а ребра другого равны \(a, a\) и \(b\) . На сколько площадь полной поверхности первого параллелепипеда больше, чем площадь поверхности второго параллелепипеда, если \(a=1000, b=1001\) .

Площадь полной поверхности первого параллелепипеда \[S_1=2(ab+b^2+ab)\] Площадь полной поверхности второго параллелепипеда \[S_2=2(ab+ab+a^2)\] Следовательно, \[S_1-S_2=2(b^2-a^2)=2(b-a)(b+a)=2(1001-1000)(1001+1000)=4002.\]

Уровень задания: Равен ЕГЭ

Дан прямоугольный параллелепипед \(ABCDA_1B_1C_1D_1\) . Во сколько раз объем пирамиды \(AA_1BD\) меньше объема этого параллелепипеда?

Пусть \(AB=x\) , \(AD=y\) , \(AA_1=z\) . Тогда объем параллелепипеда равен \[V_=S_\cdot AA_1=xy\cdot z.\] Так как \(S_=0,5S_\) (потому что по определению прямоугольного параллелепипеда в основании лежит прямоугольник), то объем пирамиды \[V_=\dfrac13\cdot S_\cdot AA_1= \dfrac13\cdot \dfrac12xy\cdot z=\dfrac16xyz.\] Следовательно, объем пирамиды в 6 раз меньше объема параллелепипеда.

Уровень задания: Равен ЕГЭ

В прямоугольном параллелепипеде диагональ грани \(AA_1D_1D\) равна \(5\) , а \(AB=2\sqrt6\) . Найдите диагональ параллелепипеда.

Так как параллелепипед прямоугольный, то все его грани – прямоугольники, а у прямоугольника обе диагонали равны. Следовательно, \(A_1D=AD_1\) . Рассмотрим диагональ \(A_1D\) и диагональ параллелепипеда \(B_1D\) . Треугольник \(A_1B_1D\) прямоугольный, так как ребро \(A_1B_1\) перпендикулярно грани \(AA_1D_1D\) (по определению прямоугольного параллелепипеда). Следовательно, гипотенуза \[B_1D=\sqrt=\sqrt=7.\]

Уровень задания: Равен ЕГЭ

Дан прямоугольный параллелепипед с ребрами \(2, \ 3\) и \(6\) . Найдите его диагональ.

Пусть \(AB=2, AD=3 , AA_1=6\) .

По теореме Пифагора из прямоугольного треугольника \(ABD\) ( \(\angle A=90^\circ\) ) имеем: \(BD^2=AB^2+AD^2\) .

Из прямоугольного треугольника \(BB_1D\) ( \(\angle B=90^\circ\) ) по теореме Пифагора \(B_1D^2=BD^2+BB_1^2\) .

Подставляя \(BD^2\) из первого равенства во второе, получим:

\[B_1D^2=AB^2+AD^2+BB_1^2=2^2+3^2+6^2=4+9+36=49 \quad \Leftrightarrow \quad B_1D=7.\]

Уровень задания: Равен ЕГЭ

Найдите объём фигуры, получившейся после удаления маленького прямоугольного параллелепипеда из большого.

Объём оставшейся фигуры равен разности объёмов большого прямоугольного параллелепипеда (каким он был до удаления) и маленького (удалённого).

Таким образом, искомый объём равен \[0,8\cdot 1\cdot 1,2 - 0,3\cdot 0,5\cdot 0,55 = 0,8775\,.\]

Мои задачи Добавить папку Мои задачи

Учащимся старших классов будет полезно научиться решать задачи ЕГЭ на нахождение объема и других неизвестных параметров прямоугольного параллелепипеда. Опыт предыдущих лет подтверждает тот факт, что подобные задания являются для многих выпускников достаточно сложными.

При этом понимать, как найти объем или площадь прямоугольного параллелепипеда, должны старшеклассники с любым уровнем подготовки. Только в этом случае они смогут рассчитывать на получение конкурентных баллов по итогам сдачи единого госэкзамена по математике.

Примеры задач

Задание 1
Найдите площадь поверхности куба, если длина его ребра составляет 12 см.

Решение:
Используем первую формулу выше и получаем:
S = 6 ⋅ (12 см) 2 = 864 см 2 .

Задание 2
Площадь поверхности куба равняется 294 см 2 . Вычислите длину его ребра.

Решение:
Примем ребро куба за a. Из формулы расчета площади следует:

Задание 3
Вычислите площадь поверхности куба, если диагональ его грани равняется 5 см.

Решение:
Воспользуемся формулой, в которой задействована длина диагонали:
S = 6 ⋅ (5 см : √ 2 ) 2 = 75 см 2 .

05. Составные многогранники. Площадь поверхности. Объем

Задача 1. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности многогранника равна разности площади поверхности прямоугольного параллелепипеда с измерениями и и двух площадей квадратов х

Если подробнее, – то так:

Задача 2. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности указанного многогранника равна площади поверхности прямоугольного параллелепипеда с измерениями xx

Задача 3. Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Площадь поверхности указанного многогранника состоит из трех пар фигур:

Задача 4. Из единичного куба вырезана правильная четырехугольная призма со стороной основания и боковым ребром Найдите площадь поверхности оставшейся части куба.

Площадь поверхности оставшейся части куба есть сумма площади поверхности куба (ребро ) и площади боковой поверхности призмы, уменьшенная на двойную площадь квадрата (со стороной ).

Задача 5. Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в раз?

При увеличении всех ребер в раз площадь каждой грани изменится в раз, поэтому и сумма площадей всех граней (площадь поверхности) увеличенного октаэдра будет в раз больше площади поверхности исходного октаэдра.

Задача 6. Площадь поверхности тетраэдра равна Найдите площадь поверхности многогранника, вершинами которого являются середины сторон данного тетраэдра Видео*

Поверхность искомого многогранника состоит из 8 граней – треугольников.

Площадь каждого такого треугольников из пары (на рисунке выделены одним цветом) в раза меньше площади соответсвующей грани тетраэдра.

Тогда (подробнее смотри в видео) сумма площадей граней многогранника есть половина поверхности тетраэдра. То есть

Задача 7. Найдите объем пространственного креста, изображенного на рисунке и составленного из единичных кубов.

Объем данного пространственного креста – есть объемов единичных кубов. Поэтому

Задача 8. Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).

Объем данного многогранника – есть объем прямоугольного параллелепипеда с измерениями и без объема прямоугольного параллелепипеда с измерениями

Задача 9. Объем тетраэдра равен Найдите объем многогранника, вершинами которого являются середины сторон данного тетраэдра.

Объем многогранника, вершинами которого являются середины сторон данного тетраэдра – разность объемов исходного тетраэдра и объемов четырех тетраэдров, объем каждого из которых составляет объема исходного тетраэдра (так как объемы подобных тел относятся друг к другу как куб коэффициента подобия).

Задача 10. Найдите объем многогранника, вершинами которого являются точки правильной треугольной призмы , площадь основания которой равна 3, а боковое ребро равно 7.

Объем многогранника, вершинами которого являются точки правильной треугольной призмы , есть разность объемов призмы и тетраэдра :

Базовая информация

Объем куба равняется кубу длины его грани. Для его расчета используется формула: V = a 3 , где V — объем куба, a — длина его грани.
Объем призмы равняется произведению площади основания фигуры на высоту. Чтобы его рассчитать, воспользуйтесь следующий формулой: V = S_o h, где V — объем призмы, So — площадь ее основания, h — ее высота.
Объем прямоугольного параллелепипеда равняется произведению его длины, ширины и высоты. Формула для его расчета: V = a · b · h, где a — длина, b — ширина, h — высота.
Объем пирамиды равняется трети от произведения площади ее основания на высоту. Рассчитать его можно по формуле: V = 1/3 S_o· h , где V — объем пирамиды, So — площадь основания пирамиды, h — длина высоты пирамиды.
Объем цилиндра равняется произведению площади его основания на высоту. Формулы для его расчета: V = π R 2 h
V = S_o h

Готовьтесь к ЕГЭ вместе со «Школково»!

Чтобы занятия проходили легко и максимально эффективно, выбирайте наш математический портал. Здесь вы найдете весь необходимый материал, который потребуется на этапе подготовки к единому государственному экзамену.

Специалисты образовательного проекта «Школково» предлагают пойти от простого к сложному: сначала мы даем теорию, основные формулы и элементарные задачи с решением, а затем постепенно переходим к заданиям экспертного уровня. Вы можете потренироваться, например, с решением задач на тему “Призма”.

Нужную базовую информацию вы найдете в разделе «Теоретическая справка». Вы также можете сразу приступить к решению задач по теме «Прямоугольный параллелепипед» в онлайн-режиме. В разделе «Каталог» представлена большая подборка упражнений разной степени сложности. База заданий регулярно пополняется.

Проверьте, легко ли вы сможете найти объем прямоугольного параллелепипеда, прямо сейчас. Разберите любое задание. Если упражнение дается вам легко, переходите к более сложным задачам. А если возникли определенные сложности, рекомендуем вам планировать свой день таким образом, чтобы ваше расписание включало занятия с дистанционным порталом «Школково».

05. Куб. Параллелепипед

Задача 2. Найдите угол прямоугольного параллелепипеда, для которого . Ответ дайте в градусах.

По т. Пифагора из треугольника :

Значит прямоугольный треугольник – равнобедренный

Почему треугольник прямоугольный?

Нам дан прямоугольный параллелепипед, значит ребро перпендикулярно грани

Тогда перпендикулярно любой прямой плоскости , в частности, по свойству прямой, перпендикулярной плоскости

Задача 3. В прямоугольном параллелепипеде известны длины рёбер Найдите синус угла между прямыми и

Угол между скрещивающимися прямыми , – это угол между и так как

Задача 4. Площадь поверхности куба равна Найдите его диагональ.

Для куба с ребром площадь поверхности такова:

Поэтому, согласно условию

Нам же требуется найти диагональ куба (, например).

Задача 5. Объем куба равен Найдите площадь его поверхности.

Для куба с ребром

По условию объем куба равен , поэтому

Для куба с ребром площадь поверхности такова:

Задача 6. Диагональ куба равна . Найдите его объем.

Как мы знаем из задачи 1, диагональ куба с ребром находится следующем образом:

По условию диагональ куба равна Поэтому

Задача 7. Во сколько раз увеличится объем куба, если его ребра увеличить в десять раз?

Если ребро куба увеличить в раз, то получим куб, подобный первоначальному (с коэффициентом подобия ). Объемы подобных тел находятся в отношении где – коэффициент подобия. Таким образом, объем увеличится в раз.

Задача 8. Если каждое ребро куба увеличить на , то его площадь поверхности увеличится на Найдите ребро куба.

Пусть ребро исходного куба равно , тогда ребро увеличенного куба равно площадь поверхности –

Так как площадь поверхности куба с ребром равна , то

разность площадей поверхностей кубов есть

По условию разность площадей поверхностей кубов равна 594, поэтому

Задача 9. Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в раза?

Если ребро куба увеличить в раза, то получим куб, подобный первоначальному (с коэффициентом подобия ). Площади поверхностей подобных тел находятся в отношении где – коэффициент подобия. Таким образом, площадь поверхности увеличится в раз.

Задача 10. Объем одного куба в раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Объемы подобных тел находятся в отношении где – коэффициент подобия.

Площади поверхностей подобных тел находятся в отношении где – коэффициент подобия.

Поэтому площадь поверхности первого куба в раза больше площади поверхности второго.

Задача 11. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Площадь поверхности этого параллелепипеда равна Найдите третье ребро, выходящее из той же вершины.

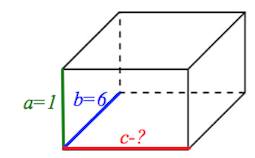
Пусть известные ребра – и , искомое ребро – .

Подставляем в формулу известные величины:

Задача 12. Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Найдите ребро равновеликого ему куба.

Для прямоугольного параллелепипеда:

Пусть ребро куба – Тогда

Задача 13. Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны и Диагональ параллелепипеда равна Найдите объем параллелепипеда.

где – ребра параллелепипеда, –диагональ.

Исходя их условия, получаем:

Задача 14. Площадь грани прямоугольного параллелепипеда равна Ребро, перпендикулярное этой грани, равно Найдите объем параллелепипеда.

Объем прямоугольного параллелепипеда (прямой призмы) равен

где – высота призмы (в данном случае – ребро, перпендикулярное грани, площадь которой известна).

Задача 15. В прямоугольном параллелепипеде известны длины рёбер: Найдите площадь сечения параллелепипеда плоскостью, проходящей через точки и

Сечение прямоугольного параллелепипеда плоскостью, проходящей через точки и – это прямоугольник

Задача 16. Диагональ прямоугольного параллелепипеда равна и образует углы , и с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Пусть рассматриваемая диагональ – .

Угол между диагональю и плоскостью нижнего основания – есть угол , так как – проекция наклонной на плоскость основания.

Угол между диагональю и плоскостью боковой грани – есть угол так как – проекция наклонной на плоскость .

Аналогично угол между диагональю и плоскостью грани – есть угол

Пусть (если градусные меры углов распределяться иначе (в другом порядке), – это никак не повлияет на решение).

Прямоугольный треугольник – равнобедренный с гипотенузой поэтому его катеты равны (например потому, что , откуда ).

Итак, ребра прямоугольного параллелепипеда равны

Тогда объем параллелепипеда равен

Задача 17. В прямоугольном параллелепипеде ребро , ребро , ребро . Точка — середина ребра Найдите площадь сечения, проходящего через точки .

Плоскость сечения () пересекает параллельные грани куба по параллельным отрезкам.

Поэтому четырехугольник (требуемое сечение) – параллелограмм. Более того, , так как перпендикулярно грани

А параллелограмм с прямым углом – это прямоугольник.

Из прямоугольного треугольника

Задача 18. Одна из граней прямоугольного параллелепипеда — квадрат. Диагональ параллелепипеда равна и образует с плоскостью этой грани угол °. Найдите объем параллелепипеда.

Пусть – квадрат, – заданная диагональ.

Проекция на – поэтому

Но тогда как катет против угла в равен половине гипотенузы то

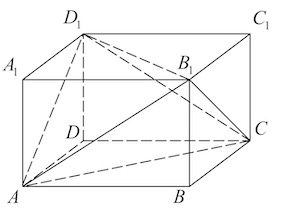
Задача 19. Найдите объем многогранника, вершинами которого являются точки параллелепипеда у которого

Многогранник с вершинами в точках – пирамида с основанием

Задача 20. Найдите объем параллелепипеда , если объем треугольной пирамиды равен

Пусть основание параллелепипеда – .

где – высота параллелепипеда.

(высота у пирамиды такая же, что и у параллелепипеда)

При этом основание пирамиды – половина основания параллелепипеда:

Итак, получаем, что

Задача 21. Найдите объем многогранника, вершинами которого являются точки прямоугольного параллелепипеда у которого

– прямая треугольная призма.

Задача 22. Найдите объем многогранника, вершинами которого являются точки параллелепипеда у которого

Задача 23. Объем параллелепипеда равен Найдите объем треугольной пирамиды

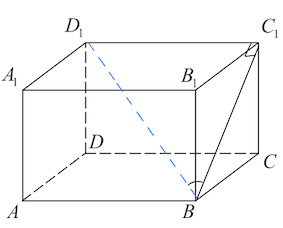
Задача 24. В кубе точка — середина ребра , точка — середина ребра , точка — середина ребра Найдите угол . Ответ дайте в градусах.

Рассмотрим треугольники . Они прямоугольные, равнобедренные, при этом все катеты равны половине ребра куба.

То есть треугольники равны друг другу.

Значит, равны и гипотенузы этих треугольников как соответствующие элементы равных треугольников.

То есть треугольник – равносторонний, а значит

Вы можете пройти тест

Автор: egeMax | комментариев 19

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Похожие статьи на сайте.

05. Призма
05. Составные многогранники. Площадь поверхности. Объем
05. Комбинации тел
05. Пирамида
05. Конус
05. Составные многогранники. Углы и расстояния

Анатолий Шевелев

Давайте разбираться! Где застряли?

Анатолий Шевелев

Ну да, любую грань можно счесть за основание, ведь площадь его (основания) фигурирует в объеме. Нам удобнее взять именно ту грань, о которой говорится в условии..

Анатолий Шевелев

Нахождение площади поверхности куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти площадь поверхности куба и разберем примеры решения задач для закрепления материала.

Содержание скрыть

Формула вычисления площади куба
- 1. Через длину ребра
- 2. Через длину диагонали грани
Основные нюансы, которые стоит запомнить
- Параллелограммы, из которых состоит параллелепипед, являются его гранями, их стороны — ребрами. Вершины этих фигур считаются вершинами самого многогранника.
- Все диагонали прямоугольного параллелепипеда равны. Так как это прямой многогранник, то боковые грани представляют собой прямоугольники.
- Так как параллелепипед — это призма, в основании которой находится параллелограмм, эта фигура обладает всеми свойствами призмы.
- Боковые ребра прямоугольного параллелепипеда перпендикулярны основанию. Следовательно, они являются его высотами.
Что такое куб: определение, свойства, формулы

В публикации мы рассмотрим определение и основные свойства куба, а также формулы, касающиеся данной геометрической фигуры (расчет площади поверхности, периметра ребер, объема, радиуса описанного/вписанного шара и т.д.).
Содержание скрыть
- Определение куба
- Свойства куба
  - Свойство 1
  - Свойство 2
  - Свойство 3
  - Диагональ
  - Диагональ грани
  - Площадь полной поверхности
  - Периметр ребер
  - Объем
  - Радиус описанного вокруг шара
  - Радиус вписанного шара
  Читайте также: