Высота в кубе как провести

Обновлено: 10.01.2025

Введите стоимость за 1 м 3 в рублях (цену кубометра):

Полная стоимость данной объема равна:

Таблица перевода куба

Для перевода полученного значения может использоваться специальный калькулятор или таблица.

м 3	дм 3	см 3	мм 3	л
1	1000	1000000	1000000000	1000

Приведенная выше информация указывает на то, что кубометр является важной единицей измерения, которая может применяться в различных сферах. Ее начинают изучать в школе, после этого она применяется в высшей математике, при профессиональной или другой деятельности.

Штрихование

Основная задача рисунка – это передать объем. Внимательно посмотрите на предмет, определите для себя тональность каждой из сторон.

Штриховать следует по форме куба. Внимательно подходите к штриховке, не стоит излишне чернить, все-таки мы рисуем гипсовый куб.

Набирайте тон постепенно, не старайтесь все сделать за один подход. Штрихи можно накладывать и в диагональном направлении.

Используйте карандаши разной мягкости. Для освещённой стороны отлично подойдет твердый карандаш – H, для полутона – HB, а для теневой стороны – B.

В некоторых случаях карандаши стоит выбирать индивидуально: некоторые люди имеют «легкую» руки и штрихуют еле заметно, а есть те, кто с помощью HB может довести рисунок до черноты.

Формулы

Для того чтобы определить рассматриваемый показатель, достаточно использовать всего одну простейшую формулу. Она используется для определения вместимости V = L × W × H, где:

L – длина;
W – ширина;
H – высота.

Правильный расчет емкости цилиндрических объектов намного сложнее. Для этого применяется следующая формула вычисления объема V= (3,14) × R2 × L, где:

R – радиус;
L – высота;
3,14 – число Пи.

Кубовый метод измерения поможет для определения объема сфер. В данном случае V = ¾ × 3,14 × R3, где:

R – радиус;
3,14 – число Пи.

Приведенная выше информация определяет то, что для измерения вместительности шара требуется только радиус. Считаться он может путем замера диаметра, который делится пополам.

При необходимости можно провести расчет значения для конуса. Формула выглядит следующим образом V = 1/3 × R2 × H, где:

R – радиус основания;
H – высота.

Формула указывает на то, что объем конуса равен 1/3 вместимости цилиндра. Для вычисления рассматриваемого показателя более сложных фигур их разбивают на несколько простых, после чего вычисляется кубометр путем сложения полученных результатов. Поэтому чтобы вычислить кубический метр, нужно рассмотреть тип геометрической фигуры.

Шаг 2 — Сокращение

Плоскости в кубе заметно удаляются в силу перспективного сокращения. Чтобы верно определить это сокращение на листе, необходимо определить углы наклона ребер.

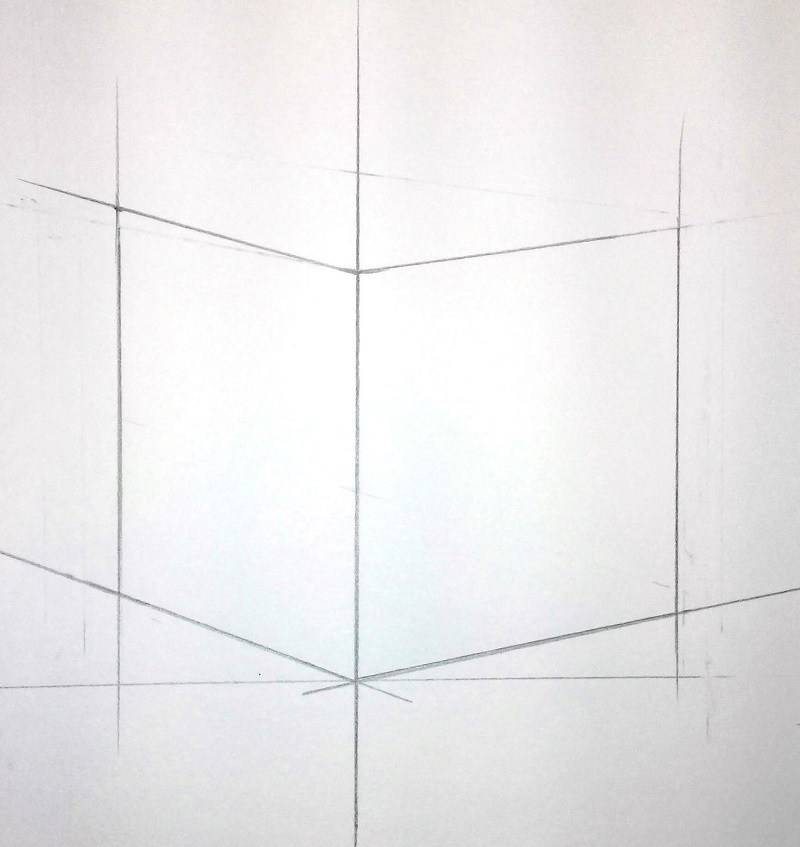
Проводим горизонтальную линию, параллельную листу бумаги, она поможет определить какой угол меньше, а какой больше. Тренируйте свой глаз, переводите взгляд с куба на рисунок, таким образом, перепроверяя себя.

Формулы для нахождения высоты треугольника

В данной публикации мы рассмотрим формулы, с помощью которых можно найти высоту в различных видах треугольников, а также разберем примеры решения задач для закрепления материала.

Содержание скрыть

Нахождение высоты треугольника
- Высота в разностороннем треугольнике
- Высота в равнобедренном треугольнике
- Высота в прямоугольном треугольнике
- Высота в равностороннем треугольнике
Как посчитать кубические метры?

Для того, чтобы перевести из метров в метры кубические, необходимо перемножить ширину, длину и высоту в метрах

1 м 3 = 1 м *1 м *1 м

Рассчитать объём в кубических метрах можно по простой формуле:

S = b * l * h

Полную стоимость всего объема можно найти по формуле:

С = V * q, где

Что такое кубический метр (кубометр)

Кубический метр – термин, который получил название от слов куб и метр. Для указания куба применяется специальный символ «³». В большинстве случаев он используется для определения объема. Куб считается фигурой трехмерного пространства, то есть он характеризуется тремя основными показателями: длиной, шириной и высотой. Поэтому стандартный кубометр –это небольшой кубик.

Один кубический метр равен 1000 литров. Высота, ширина и длина составляют по одному метру, в результате чего получается фигура для вычисления объема. Термин использовался для создания распространенного показателя Еврокуб, который сегодня активно применяется в промышленности при перевозке сыпучих и других грузов.

Подобное понятие получило широкое распространение. Его часто используют на рынке строительных материалов или в других случаях, к примеру, в квитанциях на оплату коммунальных платежей.

Более широкое распространение термин получил в математике. Многие задачи связаны с определением вместимости различных геометрических фигур. Несмотря на название, параметр подходит для расчета емкости цилиндра, сферы и других сложных форм.

Нахождение высоты треугольника

Напомним, высота треугольника – это отрезок, проведенный перпендикулярно из вершины фигуры к противоположной стороне.

Высота в разностороннем треугольнике

Высоту треугольника abc, проведенного к стороне a, можно найти по формулам ниже:

1. Через площадь и длину стороны

где S – площадь треугольника.

2. Через длины всех сторон

где p – это полупериметр треугольника, который рассчитывается так:

3. Через длину прилежащей стороны и синус угла

4. Через стороны и радиус описанной окружности

где R – радиус описанной окружности.

Высота в равнобедренном треугольнике

Длина высоты h_a, опущенной на основание a равнобедренного треугольника, рассчитывается по формуле:

Высота в прямоугольном треугольнике

Высота, проведенная к гипотенузе, может быть найдена:

1. Через длины отрезков, образованных на гипотенузе

2. Через стороны треугольника

Примечание: две остальные высоты в прямоугольном треугольнике являются его катетами.

Высота в равностороннем треугольнике

Для равностороннего треугольника со стороной a формула расчета высоты выглядит следующим образом:

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Нахождение объема куба: формула и задачи

В данной публикации мы рассмотрим, как можно найти объем куба и разберем примеры решения задач для закрепления материала.
Содержание скрыть
- Формула вычисления объема куба
- Примеры задач
Рисуем пошагово

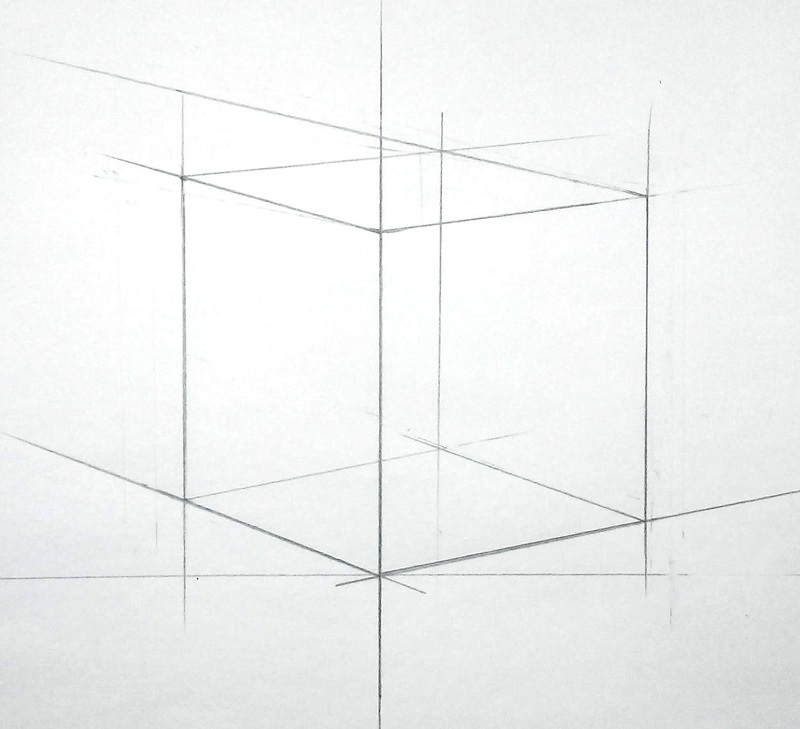
Чтобы было проще воспринять последовательность действий, давайте нарисуем куб пошагово.

Прежде чем заниматься перспективой куба, нужно наметить верные размеры предмета и определить его положение в листе. Куб не должен быть слишком маленьким или, наоборот, слишком большим.

Формула вычисления объема куба

1. Через длину ребра

Объем (V) куба равняется произведению его длины на ширину на высоту. Т.к. данные величины у куба равны, следовательно, его объем равен кубу любого ребра.

V = a ⋅ a ⋅ a = a 3

2. Через длину диагонали грани

Как мы знаем, грани куба равны между собой и являются квадратом, сторона которого может быть найдена через длину диагонали по формуле: a=d/√ 2 .

Следовательно, вычислить объем куба можно так:

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Как построить куб в перспективе: пошаговый метод

Здравствуйте, подписчики моего блога!

Многие сталкивались со сложностью в рисовании, когда хотели изобразить сложный по форме объект. Дело в том, что в основе всех сложных структур скрываются простые формы. И куб – одна из таких форм. Сегодня мы подробно разберем, как построить куб.
Содержание
Примеры задач

Задача 1
Найдите высоту треугольника, проведенную из вершины B к стороне AC, если известно, что AB = 7 см, а угол BAC = 45°.

Решение
В данном случае нам поможет формула для нахождения высоты через сторону и синус прилежащего угла:

Задача 2
Найдите длину основания равнобедренного треугольника, если высота, проведенная к нему, равняется 3 см, а боковые стороны – 5 см.

Решение
Вывести формулу для нахождения длины основания можно из формулы расчета высоты в равнобедренном треугольнике:

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Шаг — 3 — Линейная перспектива

Чтобы куб «лег» в пространство, ребра, удаленные от нас, мы рисуем выше и меньше. Этот прием лежит в основе линейной перспективы. Найдите, где заканчиваются эти ребра и обозначьте их точками. Сечение куба по трем точкам – это верных способ при построении.

Соединяем горизонтальными линиями пересечения плоскостей в кубе. Помните о том, что они сокращаются, и, если, мы их продлим, то они сойдутся в точке схода.

Невидимые грани мы также должны нарисовать. При правильном построении нужно проверить все сокращения, чтобы не было обратной перспективы.

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Примеры задач

Задание 1
Вычислите объем куба, если его ребро равняется 5 см.

Решение:
Подставляем в формулу заданное значение и получаем:
V = 5 см ⋅ 5 см ⋅ 5 см = 125 см 3 .

Задание 2
Известно, что объем куба равен 512 см 3 . Найдите длину его ребра.

Решение:
Пусть ребро куба – это a. Выведем его длину из формулы расчета объема:

Задание 3
Длина диагонали грани куба составляет 12 см. Найдите объем фигуры.

Решение:
Применим формулу, в которой используется диагональ грани:

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.

Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Куб - свойства, виды и формулы

Среди многогранников куб – это один из наиболее известных объектов, знакомых с далёкого детства. Более подробно эта тема изучается на уроках геометрии в старших классах, когда от фигур на плоскости переходят к телам в пространстве.
Содержание:
- Элементы куба
- Объем куба
- Периметр куба
- Площадь поверхности
- Сфера, вписанная в куб
- Сфера, описанная вокруг куба
- Координаты вершин куба
- Свойства куба
Кубу можно дать определение различными способами, каждый из которых только подчеркнёт тот или иной класс тел в пространстве, выделит основные признаки и особенности:

многогранник, у которого все рёбра равны, а грани попарно перпендикулярны;

прямая призма, все грани которой есть квадраты;

прямоугольный параллелепипед, все рёбра которого равны.

Всеми этими и многими другими подобными формулировками геометрия позволяет описывать одну и ту же фигуру в пространстве.

Периметр куба

Сумма длин всех рёбер равна:

Падающая тень

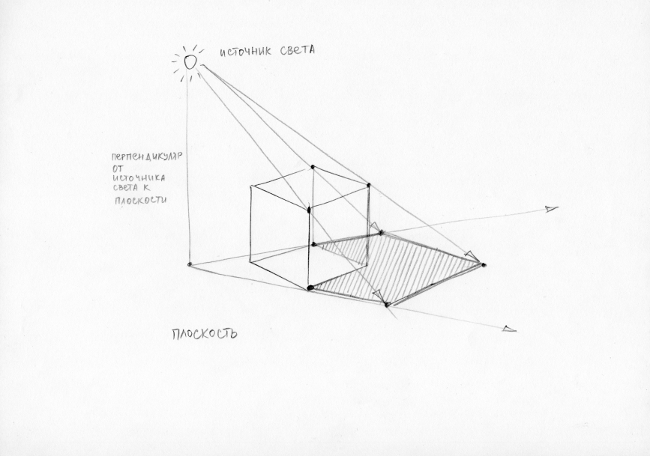
Как построить тень от куба? Чтобы падающая тень была убедительной, давайте рассмотрим основные принципы построения тени на поверхности листа.
1. Определяем местонахождения источника света.
2. Проводим перпендикуляр от источника света к плоскости, где находится наш предмет.
3. От точки, где перпендикуляр пересекается с плоскостью, проводим линии в касание с углами куба.
4. Проецируем воображаемые лучи от источника света, которые проходят по вершинам 5 куба. Намечаем точки соприкосновения лучей и плоскости.
5. Соединяем найденные точки на плоскости и получаем конфигурацию тени.
Падающая тень всегда темнее, чем собственная тень на предмете. Чем ближе она подходит к объекту, тем темнее она становится.

На самом кубе тон становится также активнее на границе двух плоскостей – освещенной и теневой. Теневая сторона, по мере удаления в пространство, высветляется за счет отраженного света от поверхности. Рефлексы помогают передать световоздушное пространство.

Шаг 1 — Композиция

Композиция – это начало любой работы. От точного нахождения композиции зависит 50% успеха работы.

Следует оставить чуть больше расстояния сверху, чем снизу. Это придаст ощущение весомости.

Начинаем рисунок с самого ближнего к нам ребра куба. Наметьте его так, чтобы оно не совпадало с центром листа. Легкими засечками определяем высоту этого ребра. Так как оно находится ближе всего, его высота будет больше остальных ребер.

Заключение

Мы поговорили о сечении куба плоскостью, о том, как правильно построить куб с натуры в перспективе. Рисование простых геометрических тел весьма полезно для начинающих и тех, кто хочет овладеть академическим рисунком.

Геометрия и расположение плоскостей в пространстве очень хорошо тренирует зрительное восприятие.

Если у вас нет гипсового куба, не беда, смастерите куб из бумаги. Для первых упражнений главное – это понять основные принципы при построении. А затем, можно будет перейти к гипсовым фигурам.

Калькулятор кубов онлайн

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

На этой странице представлен самый простой онлайн калькулятор расчета кубов по длине, ширине и высоте. Объем куба не зависит от единицы его измерения.

Сфера, вписанная в куб

Такая сфера имеет центр, совпадающий с центром куба.

Радиус равен половине ребра:

Площадь поверхности

Сумма площадей всех граней называется площадью поверхности куба. Она равна:

Элементы куба

Основными элементами многогранника считаются грани, рёбра, вершины.

Грань

Плоскости, образующие поверхность куба, называются гранями. Другое название – стороны.

Интересно, сколько граней у куба и каковы их особенности. Всего граней шесть. Две из них, параллельные друг другу, считаются основаниями, остальные – боковыми.

Грани куба попарно перпендикулярны, являются квадратами, равны между собой.

Ребро

Линии пересечения сторон называются рёбрами.

Не каждый школьник может ответить, сколько рёбер у куба. Их двенадцать. Они имеют одинаковые длины. Те из них, что обладают общим концом, расположены под прямым углом по отношению к любому из двух остальных.

Рёбра могут пересекаться в вершине, быть параллельными. Не лежащие в одной грани ребра, являются скрещивающимися.

Вершина

Точки пересечения рёбер называются вершинами. Их число равно восьми.

Центр грани

Отрезок, соединяющий две вершины, не являющийся ребром, называется диагональю.

Пересечение диагоналей грани считается центром грани – точкой, равноудалённой от всех вершин и сторон квадрата. Это есть центр симметрии грани.

Центр куба

Пересечение диагоналей куба является его центром – точкой, равноудалённой от всех вершин, рёбер и сторон многогранника.

Это есть центр симметрии куба.

Ось куба

Рассматриваемый многогранник имеет несколько осей ортогональной (под прямым углом) симметрии. К ним относятся: диагонали куба и прямые, проходящие через его центр параллельно рёбрам.

Диагональ куба

Отрезок, соединяющий две вершины, не принадлежащие одной стороне, называется диагональю рассматриваемого многогранника.

Учитывая, что ребра куба имеют равные измерения a, можно найти длину диагонали:

Формула доказывается с помощью дважды применённой теоремы Пифагора.

Диагональ куба - одна из осей симметрии.

Все диагонали куба равны между собой и точкой пересечения делятся пополам.

Диагональ грани куба

Длина диагонали грани в √2 раз больше ребра, то есть:

Эта формула доказывается также с помощью теоремы Пифагора.

Сфера, описанная вокруг куба

Как для вписанной сферы, центр совпадает с точкой пересечения диагоналей, радиус равен половине диагонали:

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

Прочие свойства:

у куба все грани равны, являются квадратами;

у куба все рёбра равны;

один центр и несколько осей симметрии.

Свойства куба

Плоскость, рассекающая куб на две части, есть сечение. Его форма выглядит как выпуклый многоугольник.

Построение сечений необходимо для решения многих задач. Как правило, используется метод следов или условие параллельности прямых и плоскостей.

Периметр куба

Сумма длин всех рёбер равна:

Единица измерения куба

Куб считается распространенной геометрической фигурой, используемой для измерения объема и определения других показателей. Однако она не может использоваться для определения площади, так как для расчета требуется только длина и ширина. Особенности кубометра заключаются в следующем:
- В качестве стандарта используется фигура, которая имеет метровые грани. Для обозначения применяется символ «³», сокращение в письменном виде «куб. м».
- При необходимости можно провести перевод полученного показателя в дециметры или сантиметры, миллиметры, километры и литры.
- В некоторых странах вычисления проводятся в футах, баррелях и ярдах. При этом перевод приблизительный, так как целое число при конвертации не получается.
- Кубометр является производной в Международной системе единиц и системе МКГСС и МТС. Поэтому в большинстве случаев производить перевод не нужно.
Единица измерения встречается в различных программах для компьютера, калькуляторах и другой вычислительной технике. Кубометровый показатель указывается на этикетке производителями материала, на емкостях и в иных случаях.

Расчет объема стены

Объем - это количественная характеристика пространства, занимаемого телом, конструкцией или веществом.

Формула расчета объема:

А - длина;
В - ширина;
С - высота.

Быстро выполнить эту простейшую математическую операцию можно с помощью нашей онлайн программы. Для этого необходимо в соответствующее поле ввести исходное значение и нажать кнопку.

В нашей проектной организации Вы можете заказать расчет объема стены на основании технологического или конструкторского задания.

На этой странице представлен самый простой онлайн калькулятор расчета объема стены. С помощью этого калькулятора в один клик вы можете вычислить объем стены, если известны длина, ширина и высота.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Где используются кубические метры

Измерить кубатурой можно различные жидкости и сыпучие материалы, газы, древесину или бетон. При этом ее распространение весьма широкое, для определения количества израсходованной воды давно не используют литры. Кубичный счетчик устанавливается в доме, квартире и других сооружениях для определения количества израсходованных природных ресурсов.

В промышленности объемы в метрах кубических измеряются для правильного смешения материалов, учета их расхода. При этом они могут измеряться при использовании специальных счетчиков, которые представлены сложными конструкциями.

Провести правильно определение размера можно только при использовании соответствующих механизмов и инструментов. При этом есть возможность выполнить правильный перевод по таблице в сантиметры. Для того чтобы рассчитать вес изделия и для получения показателя в килограммах или тоннах используется формула, предусматривающая использование значения плотности.

Какой объем имеет один кубический метр

Кубометр представляет собой стандартную единицу измерения, поэтому ее часто переводят в другие. Исключением можно назвать случай измерения объема жидкости, когда требуются литры.

В одном кубе 1000 литров. Кроме этого, в подобной емкости помещается 35,3 кубических фута, 1,31 кубических ядра и 6,29 баррелей.

Что нужно для расчета кубометра

Узнать объем материала довольно просто, так как для этого требуется всего несколько параметров. Считать следует путем перемножения:

Измерить их достаточно просто, так как для этого требуется только линейка или другой подобный измерительный прибор. Сложности возникают в случае, когда нужно определить кубометры для цилиндра или конуса. Для вычислений потребуется диаметр основания.

Координаты вершин куба

В зависимости от расположения фигуры в системе координат, можно по-разному рассчитывать координаты вершин.

Наиболее часто используют следующий способ. Одна из вершин совпадает с началом координат, рёбра параллельны осям координат или совпадают с ними, координаты единичного куба в этом случае будут равны:

Такое расположение удобно для введения четырёхмерного пространства (вершины задаются всеми возможными бинарными наборами длины 4).

Калькулятор

В интернете встречается большое количество различных калькуляторов, которые могут использоваться для вычисления кубатуры. Большинство вариантов работают на основе простых формул, при написании других применяются сложные логарифмы. В подобном случае расчеты просты:
1. Открывается сайт с онлайн-калькулятором. Их довольно много, разница заключается в количестве вводимых переменных и оформлением. Точность расчетов высокая, но при применении калькулятора в строительстве рекомендуют брать полученный результат с запасом.
2. Выбирается определенное изделие. Это делается для расчета веса и других параметров, так как от типа материала зависит плотность.
3. Указываются другие требуемые параметры.
В большинстве случаев проводится вычисление объема в кубометрах по размерам одной единицы продукции. Для этого вводится длина и ширина, а также высота. Для расчета конечной стоимости материала указывается количество и цена за одну кубатуру.

Как выглядит кубический метр

Широкое распространение рассматриваемой единицы измерения определило появление большого количества различных примеров того, как она выглядит. Общие черты следующие:
- Фигура описывается 24 ребрами. Однако не стоит забывать, что в ходе вычислений может быть получено дробное значение, или термин применяется для измерения вместимости цилиндров или сфер.
- Квадратные фигуры рассчитываются проще всего. В различных учебных заведениях может встречаться куб, который используется в качестве примера для определения рассматриваемого показателя.
- Материал должен заполнять всю емкость. Поэтому кубометр позволяет посчитать только количество жидкости, газа или сыпучих, сплошных материалов. В других случаях полученный показатель не подходит для вычисления веса, особенно если материал неоднородный.
Кубокилометр и другие варианты подобной единицы также напоминают куб, но в реальной жизни встретить подобный пример практически невозможно.

Шаг 4 — Проверка пропорций

Также можно использовать метод визирования. Вы наверняка замечали, как художники вытягивают руку и измеряют пропорции? Это и есть метод визирования.

Для того, чтобы проверить пропорции, закройте один глаз, возьмите карандаш и на вытянутой руке сопоставьте его кончик с верхом переднего ребра куба. Большой палец передвиньте в то место, где ребро заканчивается.

Высота ребра найдена. Теперь, не переставляя палец, наклоните кисть руки на 90 градусов и уже по горизонтали сопоставьте величину одного ребра с другим. Таким образом вы можете проверять и другие величины.

С опытом художники измеряют пропорции «на глаз», это значит, что они обходятся без метода визирования. Их глаз настолько натренирован, что видит размеры без измерений.

Итак, линейное построение подошло к концу, а значит, мы переходим к воздушной перспективе или, проще говоря, к штрихованию.

Что такое кубический метр и где он применяется

Производные в Международной системе единиц применяются при проведении расчетов. Кубический метр – одна из самых распространенных единиц измерения, которая применяется в самых различных сферах. Без нее сложно провести строительные, монтажные работы, рассчитать требуемое количество сыпучих материалов. Правильно высчитать единицу измерения можно самостоятельно, нужно лишь знать установленные стандарты.

Объем куба

Как для любого параллелепипеда, объём куба равен произведению всех трёх измерений, которые в данном случае равны:

Перспектива

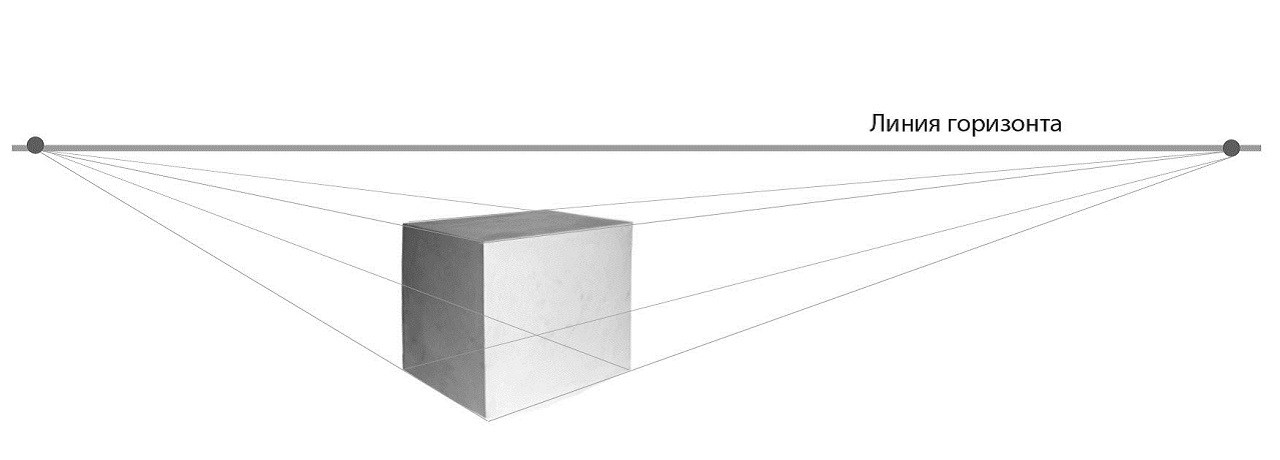
Куб – это геометрическое тело, состоящее из 6 плоскостей. Знаете, чем отличается куб от квадрата? Куб – это объемная фигура. А при рисовании любых объемных фигур нужно помнить о перспективе.

Из-за законов перспективы стороны куба будут сокращаться, иными словами становиться меньше.

Для начала нужно определить линию горизонта. Это необходимо для того, чтобы правильно построить куб в перспективе.

Линия горизонта – это уровень глаз художника. На ней будут располагаться две точки схода. В каждую из этих точек придёт по 4 линии. Наглядно такой рисунок будет выглядеть следующим образом:

Читайте также: