Куб с длиной ребра 20 см плавает в воде чему равна выталкивающая сила
\[F_A=\rho_\text g V_\text\] где \(\displaystyle V_\text\) — объём погружённой части тела, \(\displaystyle \rho_\text\) — плотность жидкости.
Рассмотрим тело плотности \(\rho\) и жидкость плотности \(\rho_0\) . Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести \(mg\) и архимедова сила \(F_A\) . Если объём тела равен V, то
\[mg=\rho g V,\] \[F_A=\rho_0 g V\]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы : \(\displaystyle mg > F_A\) , или \(\displaystyle \rho>\rho_0\) . В этом случае тело тонет.
Сила тяжести равна архимедовой силе : \(\displaystyle mg = F_A\) , или \(\displaystyle \rho=\rho_0\) . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы : \(\displaystyle mg < F_A\) , или \(\displaystyle \rho<\rho_0\) . В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства \(\displaystyle \rho\leq \rho_0\) .

Два жестко связанные друг с другом одинаковых бруска, имеющие толщину \(h=5\) см, плавают в воде так, что уровень воды приходится на границу между ними (см. рисунок). Насколько изменится глубина погружения, если на два бруска положить ещё пять таких же? (Ответ дайте в сантиметрах.)
Два одинаковых связанных бруска погрузились наполовину в воду (из условия). Пусть
\(\displaystyle\rho_1\) – плотность материала, из которого изготовлены бруски, а \(\displaystyle V\) – объем двух брусков. Тогда масса этих брусков будет равна \[\displaystyle m=\rho_1V\] Сила, с которой льдинки действуют на воду, равна силе тяжести \[\displaystyle F=mg=\rho_1Vg\] Сила, с которой бруски выталкиваются из воды, равна силе Архимеда \[F_\text=\rho g\frac2,\] где \(\displaystyle \rho\) – плотность воды, \(\displaystyle \frac2\) – объем погруженного в воду тела (бруски погружены только
наполовину). Так как они плавают на поверхности воды, то эти силы уравновешивают друг друга, значит, имеем: \[\rho_1Vg=\rho g\frac2,\] откуда \(\displaystyle \rho_1=\dfrac2,\) то есть плотность материала, из которого сделаны бруски в 2 раза меньше плотности воды. Это говорит о том, что если взять семь брусков, то они также будут погружены наполовину, то есть на величину \[\frac72h=3,5\cdot5\text< см>=17,5 \text< см>.\] Глубина увеличится на \(\displaystyle 17,5 -5=12,5\) см.
Подвешенный на нити алюминиевый кубик целиком погружен в воду и не касается дна сосуда. Плотность алюминия равна \(\displaystyle \rho_\text< ал>=2700 \text< кг>/\text^3. \) Какова длина ребра куба, если выталкивающая сила равна \(\displaystyle F_\text=33,75\text< Н>?\) (Ответ дайте в сантиметрах.)
Выталкивающая сила равна по определению \[F_\text=\rho_\text gV,\] где \(\displaystyle \rho_\text\) – плотность жидкости, в которую погружен кубик, \(\displaystyle V\) – объем погруженной части тела. Так как куб погружен целиком, то \(\displaystyle V=a^3\) , получим: \[F_\text=\rho_\text ga^3\] Выразив из этой формулы сторону \(\displaystyle a\) , получаем \[a=\sqrt[3]<\frac
Однородный цилиндр, изготовленный из материала плотностью \(\displaystyle \rho=600\) кг/м \(^3\) , с радиусом основания \(\displaystyle R=25\) см и высотой \(\displaystyle H=20\) см привязан нитью ко дну сосуда, наполненного водой. Найдите силу натяжения нити. (Ответ дайте в ньютонах.)


Сделаем рисунок с указанием сил, действующих в системе. Можем записать II закон Ньютона в векторной форме: \[\vec T+\vec F_\text+m\vec g=m\vec a,\] так как цилиндр покоится, то ускорение равно нулю, в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: \[T- F_\text+mg=0, \quad(1)\] массу цилиндра можно рассчитать, исходя из формулы \(\displaystyle \rho=\frac \Rightarrow m=\rho V,\) где V – объем цилиндра, который можно вычислить по формуле \[V=\pi R^2 H\] Из формулы (1) выразим силу натяжения нити T: \[T=F_\text-mg=\rho_\textgV-\rho gV=Vg(\rho_\text-\rho)=\pi R^2 Hg(\rho_\text-\rho),\] где \(\displaystyle \rho_\text\) – плотность воды, подставим в получившееся выражение численные значения: \[T=3,14\cdot0,25^2\text< м>\cdot0,2\text< м>\cdot 10\text< м>/\text^2 \cdot (1000\text< кг>/\text^3-600\text< кг>/\text^3)=157\text< Н >\]
Однородный кубический предмет с ребром \(\displaystyle a=18\) см опускают в эфир. На сколько сантиметров длина части стороны, находящейся под жидкостью отличается от длины части над эфиром? Плотность вещества, из которого изготовлен куб равна \(\displaystyle \rho_\text=340\) кг/м \(^3\) , плотность эфира \(\displaystyle \rho_\text=720\) кг/м \(^3\) . (Ответ дайте в сантиметрах.)
Запишем условие равновесия кубика на поверхности эфира: \[F_\text< Арх>=mg, \quad(1)\] где \(F_\text< Арх>\) – выталкивающая сила, действующая на брусок, \(\displaystyle m\) – масса кубика, которую можно рассчитать, исходя из формулы \(\displaystyle \rho_\text=\frac \Rightarrow m=\rho_\text V,\) где V – объем кубика, который можно вычислить по формуле \[V=a^3.\] Выталкивающая сила равна: \[F_\text< Арх>=\rho_\textgV_\text,\] где \(\displaystyle V_\text\) – объем погруженной части кубика, \[V_\text=xa^2,\] где \(\displaystyle x\) – длина части стороны, находящейся под эфиром, значит, выражение (1) можно записать в следующем виде: \[\rho_\textgxa^2=\rho_\texta^3\] \[\rho_\textx=\rho_\texta, \text < выразим >x=\frac<\rho_\texta><\rho_\text>.\] Пусть \(\displaystyle y\) – длина части стороны, находящейся над эфиром, можем записать: \[y=a-x,\] искомая разница длин \(\displaystyle \delta=y-x=a-2x=a-2\cdot \dfrac<\rho_\texta><\rho_\text>=a(1-2\cdot \dfrac<\rho_\text><\rho_\text>)\) подставим в получившееся выражение численные значения: \[\displaystyle \delta=0,18\text< м>(1-2\cdot \dfrac/\text^3>/\text^3>)=0,01\text< м>=1\text< см>\]
В некий резервуар было налито 1000 литров жидкости плотностью \(\displaystyle \rho_1=1500\) кг/м \(^3\) . В этой жидкости в равновесии плавает кубик, погруженный в воду на \(\displaystyle x=130\) см. Длина стороны кубика равна \(\displaystyle a=200\) см. В сосуд доливают ещё 1000 литров жидкости плотностью \(\displaystyle \rho_2=1100\) кг/м \(^3\) и перемешивают. Чему после этого будет равна длина погруженной части кубика при плавании в равновесии? Обе жидкости хорошо смешиваются, и при смешивании суммарный объём сохраняется. (Ответ дайте в метрах.)
В условии сказано, что жидкости хорошо перемешиваются. Из этого следует, что при смешивании получается новая жидкость, плотность которой является средним арифметическим изначальных, так как взятые объемы одинаковы. \[\rho_\text=\dfrac\] Так как кубик плавает на поверхности, то можно записать: \[mg=F_\text,\] сила тяжести, действующая на тело не изменяется, значит, выталкивающая сила тоже остается постоянной. Сначала сила Архимеда равна: \[F_\text=\rho_1 g V_\text,\] где \(\displaystyle V_\text=a^2x\) – объем погруженной части куба до смешивания. После смешения жидкостей в сосуде: \[F_\text=\rho_\text g V_\text=\dfracg V_\text,\] где \(\displaystyle V_\text=a^2y\) – объем погруженной части куба до смешивания, \(\displaystyle y\) – длина погруженной части стороны куба после смешивания жидкостей. Можем приравнять получившиеся выражения, получим \[\rho_1 g a^2x=\dfrac g a^2y\] \[\rho_1x=\dfracy,\] выразим отсюда y: \[y=\frac,\] подставим в получившееся выражение численные значения: \[y=\frac/\text^3 \cdot1,3\text< м>>/\text^3+1100\text< кг>/\text^3>=1,5\text< м>\]
Стеклянный шарик опускается в воде с ускорением \(\displaystyle a=6\) м/с \(^2\) . Найти плотность стекла. Плотность воды \(\displaystyle \rho_\text=1000\) кг/м \(^3\) . Силами вязкого трения пренебречь. (Ответ дайте в кг/м \(^3\) .)

При движении шарика в воде на него действует сила тяжести \(\displaystyle m\vec g\) и сила Архимеда \(\displaystyle F_\text\) . Сделаем рисунок с указанием сил, действующих в системе. Можем записать 2 закон Ньютона в векторной форме: \[\vec F_\text+m\vec g=m\vec a,\] в проекции на ось, направленную вертикально вниз, 2 закон Ньютона можно записать следующим образом: \[mg- F_\text=ma,\] Отсюда с учетом выражения для силы Архимеда \(\displaystyle F_\text=\rho_\text g V\) , где V – объем шарика, а
\(\displaystyle \rho_\text\) – плотность воды, получим: \[mg- \rho_\text g V=ma,\] Выразим массу шарика: \[m=\frac <\rho_\textg V>.\] Исходя из формулы, плотность стекла равна \[\displaystyle \rho_\text=\frac =\frac <\rho_\textg V>=\frac <\rho_\textg >,\] подставим в получившееся выражение численные значения: \[\rho_\text=\frac/\text^3\cdot 10\text< м>/\text^2 >/\text^2-6\text< м>/\text^2>=2500\text< кг>/\text^3\]
Однородный шарик, изготовленный из материала плотностью \(\displaystyle \rho=2000\) кг/м \(^3\) погружен в воду. Чему равен радиус шара, если выталкивающая сила равна
\(\displaystyle F_\text=100\) Н? (Ответ дайте в сантиметрах и округлите до целых.)
Выталкивающая сила равна по определению \[F_\text=\rho_\text gV_\text,\] где \(\displaystyle \rho_\text\) – плотность воды, \(\displaystyle V_\text\) – объем погруженной части тела. Так как шар полностью опущен в воду, то \[V_\text=\frac43\pi R^3,\] где \(\displaystyle R\) – радиус шара, получим: \[F_\text=\rho_\text g\frac43\pi R^3,\ (1)\] выразим из формулы R: \[R=\sqrt[3]<\frac<3F_\text><4\rho_\textg\pi>>\] Подставив значения в формулу, получим: \[R=\sqrt[3]> /\text^3\cdot10\text< м>/\cdot3,14>> \approx0,13\text< м>=13\text< см >\]
Куб с длиной ребра 20 см плавает в воде, наполовину погруженным в неё. Плотность воды 1000 кг/м в кубе . На куб действует выталкивающая сила, равная. Найти выталкивающую силу
Выталкивающая сила = Плотность жидкости * коэффициент g * объем погруженной части тела.1)Найдем объем кубаV = a^3 = 0.2(метра)^3 = 0.008 метра^32)Найдем объем половины кубаон равен 0.004 метра^33)Выталкивающая сила = Плотность жидкости * коэффициент g * объем погруженной части тела.Выталкивающая сила = 1000 кг/м в кубе * 10 H/кг * 0.004 метра^3 = 40H
Также наши пользователи интересуются:

⭐⭐⭐⭐⭐ Лучший ответ на вопрос «Куб с длиной ребра 20 см плавает в воде, наполовину погруженным в неё. Плотность воды 1000 кг/м в кубе . На куб действует выталкивающая сила, равная. Найти выталкивающую силу» от пользователя НИКИТА ПАВЛОВ в разделе Физика. Задавайте вопросы и делитесь своими знаниями.
Куб с длиной ребра 10 см плавает вертикально в жидкости, плотность которой 900 кг/м3. Над поверхностью жидкости выступает часть
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Куб, ребро которого 20 см, находится в воде. Нижняя грань куба удалена от поверхности воды на расстояние 1 м. Чему равна сила, действующая
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
На полу лежит алюминиевый куб с длиной ребра 20 см. Изобразите на чертеже силу тяжести, действующую на куб, и вес куба,
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Куб с длиной ребра 20 см плавает в воде чему равна выталкивающая сила
Задача № 1. Тело объемом 2 м 3 погружено в воду. Найдите архимедову силу, действующую на тело.
Задача № 2. Определить выталкивающую силу, действующую на деревянный плот объемом 12 м 3 , погруженный в воду на половину своего объема.
Задача № 3. Каков объем железобетонной плиты, если в воде на нее действует выталкивающая сила 8000 Н?
Задача № 4. Какую силу надо приложить, чтобы удержать под водой бетонную плиту, масса которой 720 кг?
Задача № 5. Какую высоту должен иметь столб нефти, чтобы уравновесить в сообщающихся сосудах столб ртути высотой 16 см?
Задача № 6. Вес тела в воздухе равен 26 кН, а в воде — 16 кН. Каков объем тела?
Задача № 7. Какую силу нужно приложить, чтобы удержать в воде кусок гранита объемом 40 дм 3 ?
Задача № 8. Определите объем куска меди, который при погружении в керосин выталкивается силой 160 Н.
Задача № 9 (повышенной сложности). Медный шар в воздухе весит 1,96 Н, а в воде 1,47 Н. Сплошной этот шар или полый?
Задача № 10 (повышенной сложности). Рассчитайте, какой груз сможет поднять шар объемом 1 м 3 , наполненный водородом. Какой примерно объем должен иметь шар с водородом, чтобы поднять человека массой 70 кг? (Вес оболочки не учитывать.)
Задача № 11. Деревянный цилиндр плавает на поверхности воды так, что он погружен в воду на 90%. Какая часть цилиндра будет погружена в воду, если поверх воды налить слой масла, полностью закрывающий цилиндр? Плотность масла 800 кг/м 3 .
Дано: V – объем цилиндра (V = Sh); h – высота цилиндра; S – площадь основания цилиндра; V1 – объем цилиндра, погруженного в масло (V1 = V – V2 = Sh1); h1 – высота части цилиндра, погруженной в масло; V2 – объем цилиндра, погруженного в воду после добавления масла; рв – плотность воды (1000 кг/м 3 ); рм – плотность масла (800 кг/м 3 )
Решение . F – сила, выталкивающая цилиндр из воды до добавления масла F = 0,9pвgV
F1 – сила, выталкивающая цилиндр из масла F1 = pмgV1
F2 – сила, выталкивающая цилиндр из воды после добавления масла F2 = pвgV2
Баланс сил: F – F1 = F2
0,9pвgV – pмgV1 = pвgV2 V1 = V – V2 ⇒ 0,9pвV – pм(V – V2) = pвV2
V(0,9pв – pм) = V2(pв – pм) V = Sh; V1 = Sh1 ⇒

Ответ: 1/2 часть цилиндра будет погружена в воду (50%).
Задача № 12. Плоская льдина плавает в воде, выступая над уровнем воды на 3 см. Человек массой 70 кг зашел на льдину. В результате, высота выступающей части над льдиной уменьшилась в 3 раза. Найти площадь льдины.
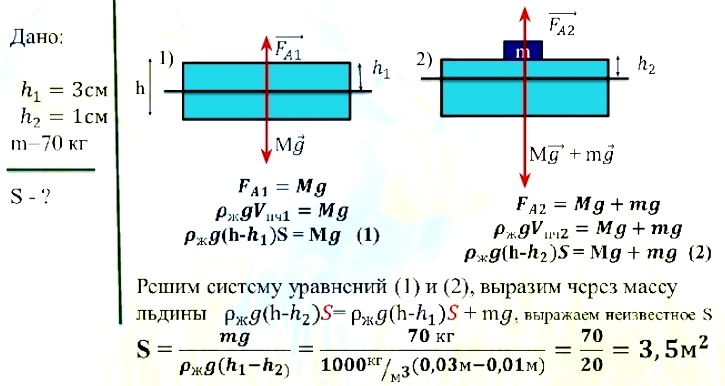
Ответ: 3,5 м 3 .
Теория для решения задач.
Давление жидкости на покоящееся в ней тело называют гидростатическим давлением. Гидростатическое давление на глубине h равно р = ратм + p*g*h
Закон Паскаля. Жидкость и газ передают оказываемое на них давление во всех направлениях одинаково.
Куб с длиной ребра 20 см плавает в воде чему равна выталкивающая сила
В сосуде с водой, не касаясь стенок и дна, плавает деревянный (сосновый) кубик с длиной ребра 20 см. Кубик вынимают из воды, заменяют половину его объёма на материал, плотность которого в 6 раз больше плотности древесины, и помещают получившийся составной кубик обратно в сосуд с водой. На сколько увеличится модуль силы Архимеда, действующей на кубик? Ответ выразите в ньютонах. (Плотность сосны — 400 кг/м 3 .)
В первом случае кубик плавает в воде, а это значит, что сила тяжести уравновешивается силой Архимеда:
После замены части кубика его средняя плотность станет равной Она больше плотности воды и значит, во втором случае кубик полностью погрузится в воду. Сила Архимеда в этом случае будет равна:
Отсюда получаем, что сила Архимеда увеличится на 48 Н.
Источник: Тренировочная работа по физике 21.03.2017, вариант ФИ10403 Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.3.5 Закон Архимеда. Условия плавания тел Денис Шостак 03.02.2018 22:01Не могу никак понять. Первый случай:
тело плавает, значит Fa=mg.
Делю обе части равенства на g и V(тела).
Остаётся: ρ(воды)=ρ(тела), чего не может быть, т.к. плотность воды - 1000, а плотность тела - 400.
Также мне непонятно, почему в решении написано, что "во втором случае он полностью погрузится в воду". Т.е. в первом случае он был не полностью погружён? В условии же написано, что тело ПЛАВАЛО - т.е. находилось полностью в водном пространстве.
И как архимедова сила может увеличиться или уменьшиться, если по закону она зависит от объёма тела? Объем куба и в первом и во втором случае одинаковый, а значит и архимедова сила тоже одинакова.
Артём КоршуновИз условия плавания тел следует, что тело плавает в жидкости, если его плотность равна плотности жидкости. Если же плотность тела меньше плотности жидкости, то тело начнет всплывать, вследствие чего уменьшится объем части тела, погруженный в жидкость, а значит уменьшится и сила Архимеда. В первом случае тело находится в равновесии и по второму закону Ньютона сила Архимеда будет в точности равна силе тяжести.
Во втором случае плотность тела становится больше плотности воды, а значит тело тонет и сила Архимеда может быть найдена по стандартной формуле.
Куб с длиной ребра 20 см плавает в воде чему равна выталкивающая сила
Кубик из резины с ребром 10 см опускают в воду. Каково отношение объёма кубика, находящегося под водой, к объёму кубика, находящегося над водой? Плотность резины 0,8 г/см 3 .
На кубик в воде действуют две силы: сила Архимеда и сила тяжести.
Второй закон Ньютона:
где — объем кубика под водой, — объем кубика над водой, — плотность воды, — плотность резины.
Поделим выражение на и выразим
Аналоги к заданию № 7345: 7377 Все
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.3.4 Давление в жидкости, покоящейся в ИСОПоскольку трения между кубиком и опорой нет, а кубик покоится (его ускорение равно нулю), второй закон Ньютона для кубика в проекции на горизонтальную ось приобретает вид:
С другой стороны, по третьему закону Ньютона, сила, с которой растягивают вторую пружину, равна возникающей в пружине силе упругости: Таким образом,
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.5 Третий закон Ньютона для материальных точек, 1.2.8 Сила упругости. Закон Гука Пашка Филатов (Москва) 10.06.2012 01:37В вопросе спрашивается на счет силы F, которая в итоге действует на всю систему.
А вторая часть решения представлена для системы, в которой кубик будто бы закреплен на плоскости.
Если посмотреть на ваше решение, можно сделать вывод, что на одну из пружин вообще не действует никакая сила и она не растягивается.
Алексей (Санкт-Петербург)Здесь все верно, поверьте мне.
Сила действует только на правую пружину, она растягивается, тянет кубик, он тянет вторую пружину, она растягивается (и тащит стенку, но стенка тяжелая и не поддается :) )
Татьяна Николаева 25.09.2012 19:00Здравствуйте, возможно,что глупый вопрос , но почему k2дельтаХ2 МИНУС k1дельтаХ1.Почему минус?
Алексей (Санкт-Петербург)Это проекция второго закона Ньютона для кубика на горизонтальную ось. Ускорения равно нулю, поэтому в правой части стоит ноль. Силы от пружинок направлены в разные стороны, поэтому проекции идут с разными знаками.
В случае статики можно подобные законы писать и иначе: силы, направленные в одну сторону, приравнивать силам, направленным в противоположную сторону. В данном случае это даст: , что, конечно, то же самое. Так что форма записи, это скорее вопрос удобства или привычки.
Задание 16 № 10645В центр верхней грани прозрачного кубика под углом α = 45° падает из воздуха луч света (см. рисунок). Плоскость падения луча параллельна плоскости передней грани кубика (АВСD). Преломлённый луч попадает в ребро АЕ кубика. Определите показатель преломления материала, из которого изготовлен кубик. Ответ округлите до сотых долей.
По закону преломления Снеллиуса синусы углов падения и преломления связаны с показателями преломления двух сред соотношением Показатель преломления воздуха можно считать равным единице. Пусть сторона куба равна a, тогда из рисунка следует, что тангенс угла преломления равен
Используя тригонометрические формулы, найдем синус этого угла
Отсюда показатель преломления кубика равен
Источник: Тренировочная работа по физике 18.09.2018, вариант ФИ10101 Раздел кодификатора ФИПИ/Решу ЕГЭ: 3.6.4 Законы преломления света. Преломление света Задание 16 № 10713В центр верхней грани прозрачного кубика под углом α = 60° падает луч света (см. рисунок). Преломлённый луч попадает в вершину А кубика. Определите показатель преломления материала, из которого изготовлен кубик.
По закону преломления Снеллиуса синусы углов падения и преломления связаны с показателями преломления двух сред соотношением Показатель преломления воздуха можно считать равным единице. Пусть сторона куба равна a, тогда из рисунка следует, что тангенс угла преломления равен
Используя тригонометрические формулы, найдем синус этого угла
Отсюда показатель преломления кубика равен
Аналоги к заданию № 10645: 10713 Все
Источник: Тренировочная работа по физике 18.09.2018, вариант ФИ10102 Задание 25 № 19905 Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.11 Уравнение теплового балансаКубик массой 2 кг покоится на гладком горизонтальном столе, сжатый с боков пружинами (см. рисунок). Левая пружина жёсткостью k1 = 500 Н/м сжата на 3 см. С какой силой правая пружина действует на кубик? Ответ приведите в ньютонах.
Кубик покоится, следовательно, равнодействующая сил, направленных на него равна нулю. По закону Гука следовательно, модуль второй силы равен модулю первой:
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.8 Сила упругости. Закон Гука Задания Д28 C1 № 7365Объём куба находится по формуле
Объем вырезанного кубика: Объём остальной части:
Значит, масса нового куба равна:
Средняя плотность находится как
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.2 Масса тела. Плотность вещества Задания Д28 C1 № 7397Объем куба находится по формуле
Объем вырезанного кубика: Объем остальной части:
Значит, масса нового куба равна:
Средняя плотность находится как
Ответ: 6750 кг/м 3 .
Аналоги к заданию № 7365: 7397 Все
Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.2 Масса тела. Плотность веществаКубик со стороной а и плотностью ρk подвешен на нерастяжимой нити и погружен в воду так, что его верхняя грань параллельна поверхности воды и находится на глубине а. Кубик не касается дна и стенок сосуда. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
А) давление воды на верхнюю грань
Б) На кубик действуют силы: натяжения нити и выталкивающая, направленные вертикально вверх, и сила тяжести, направленная вертикально вниз. Из условия равновесия следует, что По формулам архимедова сила масса тела Тогда сила натяжения
Источник: ЕГЭ — 2021 по физике. Основная волна 11.06.2021. Москва Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.3.4 Давление в жидкости, покоящейся в ИСО, 1.3.5 Закон Архимеда. Условия плавания телКубик массой M = 1 кг, сжатый с боков пружинами (см. рисунок), покоится на гладком горизонтальном столе. Первая пружина сжата на 4 см, а вторая сжата на 3 см. Жёсткость первой пружины k1 = 600 Н/м. Чему равна жёсткость второй пружины k2? Ответ выразите в ньютонах на метр.
Так как кубик покоится, то по второму закону Ньютона:
Найдем отсюда жесткость второй пружины:
Источник: Досрочный ЕГЭ по физике 2017, вариант 101 Раздел кодификатора ФИПИ/Решу ЕГЭ: 1.2.4 Второй закон Ньютона: для материальной точки в ИСО, 1.2.8 Сила упругости. Закон Гука Задания Д4 B4 № 4117Однородный сплошной кубик установлен так, что одним своим ребром он опирается на шероховатую поверхность вертикальной стены, а другим ребром - на шероховатый горизонтальный пол. Кубик находится в равновесии. На рисунке показаны силы, которые действуют на кубик. Относительно каких точек, обозначенных на рисунке, момент силы трения кубика о пол равен нулю?
Модуль силы трения отличен от нуля. Поэтому момент этой силы равен нулю только относительно таких точек, относительно которых ее плечо равно нулю. То есть нас интересуют только точки, лежащие на линии действия силы. Это точки B и C.
Кубик со стороной a = 30 см плавает на границе раздела двух несмешивающихся жидкостей, плотности которых равны ρ1 = 800 кг/м 3 и ρ2 = 1000 кг/м 3 . Объём кубика, погружённый в нижнюю жидкость, в 2 раза больше, чем объём, погружённый в верхнюю жидкость. Высота уровня первой жидкости над кубиком равна h = 10 см. Нижняя грань кубика удалена от дна сосуда на H = 20 см.
Установите соответствие между отношениями гидростатических давлений в разных указанных точках сосуда и численными значениями этих отношений. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
Гидростатическое давление столба жидкости определяется только высотой столба и плотностью жидкости
Гидростатика. Сила Архимеда (страница 2)
\[F_A=\rho_\text g V_\text\] где \(\displaystyle V_\text\) — объём погружённой части тела, \(\displaystyle \rho_\text\) — плотность жидкости.
Рассмотрим тело плотности \(\rho\) и жидкость плотности \(\rho_0\) . Допустим, тело полностью погрузили в жидкость и отпустили. Сразу после отпускания на тело действуют лишь сила тяжести \(mg\) и архимедова сила \(F_A\) . Если объём тела равен V, то
\[mg=\rho g V,\] \[F_A=\rho_0 g V\]
Имеются три возможности дальнейшего движения тела.
Сила тяжести больше архимедовой силы : \(\displaystyle mg > F_A\) , или \(\displaystyle \rho>\rho_0\) . В этом случае тело тонет.
Сила тяжести равна архимедовой силе : \(\displaystyle mg = F_A\) , или \(\displaystyle \rho=\rho_0\) . В этом случае тело остаётся неподвижным в состоянии безразличного равновесия.
Сила тяжести меньше архимедовой силы : \(\displaystyle mg < F_A\) , или \(\displaystyle \rho<\rho_0\) . В этом случае тело всплывает, достигая поверхности жидкости.
Таким образом, условие плавания тела можно записать в виде неравенства \(\displaystyle \rho\leq \rho_0\) .
Читайте также:


