Из 100 туристов отправляющихся в заграничное путешествие
По окончании соревнований оказалось, что в каждом из предположений только одно
из высказываний истинно, другое ложно.
Какое место на соревнованиях занял каждый из юношей, если все они заняли разные
места.
Из 100 туристов, отправляющихся в путешествие, немецким языком владеют 30 человек, английским — 28, французским — 42. Английским
Как быстро выучить стихотворение наизусть? Запоминание стихов является стандартным заданием во многих школах.
Как научится читать по диагонали? Скорость чтения зависит от скорости восприятия каждого отдельного слова в тексте.
Как научится говорить грамотно и правильно? Общение на хорошем, уверенном и естественном русском языке является достижимой целью.
Круги Эйлера - хороший, а главное удобный (графически иллюстрированный) способ решения текстовых задач.
В этом разделе будут рассмотрены 2 текстовых задачи, решенные этим методом.
Для полного понимания решения настоятельно рекомендуется учить все вовремя , а не как студент, выполнивший данный проект.
В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом. Сколько ребят увлекаются одновременно тремя видами спорта? Сколько ребят увлекается лишь одним из этих видов спорта?
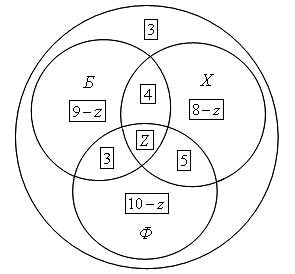
Решение: Воспользуемся кругами Эйлера.
Пусть большой круг изображает всех учащихся класса, а три меньших круга Б, Х и Ф изображают соответственно баскетболистов, хоккеистов и футболистов. Тогда фигура Z, общая часть кругов Б, Х и Ф, изображает ребят, увлекающихся тремя видами спорта. Из рассмотрения кругов Эйлера видно, что одним лишь видом спорта - баскетболом занимаются
16 - (4 + z + 3) = 9 - z;
одним лишь хоккеем
17 - (4 + z + 5) = 8 - z;
одним лишь футболом 18 - (3 + z + 5) = 10 - z;
Составляем уравнение, пользуясь тем, что класс разбился на отдельные группы ребят; количества ребят в каждой группе обведены на рисунке рамочкам:
3 + (9 - z) + (8 - z) + (10 - z) + 4 + 3 + 5 + z = 38,
z = 2.
Таким образом, двое ребят увлекаются всеми тремя видами спорта.
Складывая числа 9 - z, 8 - z и 10 - z, где z = 2, найдем количество ребят, увлекающихся лишь одним видом спорта: 21 человек.
Ответ:
Двое ребят увлекаются всеми тремя видами спорта человека.
Увлекающихся лишь одним видом спорта: 21 человек.

13 Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3.
Сколько туристов не владеют ни одним языком?

Выразим условие этой задачи графически. Обозначим кругом тех кто знает английский, другим кругом - тех, кто знает французский, и третим кругом - тех, кто знают немецкий.
Тогда, например, те, кто владеет и английским и немецким, «попадут» в общую часть первого и третьего круга.
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3. Английским и французским языками владеют 10 человек, а 3 из них владеют еще и немецким. Следовательно, только английским и французским владеют 10-3=7 человек.

Определим теперь, сколько человек владеют только одним из перечисленных языков. Немецкий знают 30 человек, но 5+3+2=10 из них владеют и другими языками, следовательно, только немецкий знают 20 человек. Аналогично получаем, что одним английским владеют 13 человек, а одним французским - 30 человек.
Ответ:
Только английским владеет 13 человек, только французским - 30, только немецким - 20 человек.
20 человек не знают ни одного из этих языков.
Домашнее задание семилетнего ребенка поставило в тупик доктора наук

Вопрос быстро набрал вирусную популярность: за сутки он получил несколько тысяч лайков и более 260 ретвитов. Некоторые пользователи ответили, что у полукруга действительно есть два прямых угла. Однако другие посчитали утверждение ложным из-за наличия изогнутых линий.
Йейтс позже нашел в интернете правильный ответ на вопрос. Авторы домашнего задания считали, что утверждение ложно. Они объяснили, что дети могут приложить фигуру к углу страницы тетради и понять, что у них получается не прямой угол.
Несмотря на найденные доказательства, доктор математических наук не согласился с ними. Он отметил, что при увеличении масштаба можно будет увидеть, что касательные к полукругу в данной точке будут составлять прямой угол с диаметром. Йейтс пообещал показать этот сложный вопрос своим студентам в университете.
Показать полностью 1 10 месяцев назад
Какой ответ верный?
Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5,
всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?
1). Способ решения
Из 100 туристов:
немецким. 30; только немецким. 30 -8 -5-3= 14
французским. 42; только французским. 42-10- 5-3=24
английским и французским. 10; только англ.и француз. 10-3= 7
немецким и французским. 5; только немец.и француз. 5-3= 2
всеми тремя языками. 3; только англ.,немец.,француз. 3
не владеют ни одним языком . ; не владеют. 100-14-7-24-5-7-2-3=38
2). Способ решения
Если всеми тремя языками владеют 3 человека, то
1. Только Н и Ф (без А) одновременно владеют 5-3 = 2 человека
2. Только А и Ф (без Н) одновременно владеют 10-3 = 7 человек
Только Н (без Ф и А) владеют 30 - (2+3+5) = 20 человек
Дубликаты не найдены
3 года назад
Вот, немного аккуратней )

Круги Эйлера же
3 года назадПравильное решение будет зависеть от наличия слова "только" в условии перед словами "английским и немецким" и тд.
Условия задачи должны быть однозначны: если вы можете трактовать условие иначе и этой трактовке не противоречат другие части условия - ваша трактовка верна, и решение согласно ей - тоже.
А на самом деле задачи обычно составляют те, кто этого в принципе правильно делать не умеет и/или не делал этого никогда в жизни.
ps. скорее всего автор задачи имел ввиду, что слово "только" там стоит, но автор - мудак.
pps. вероятно, один из вариантов решения будет некорректен просто по цифрам и тогда будет возможно только другое, но сейчас у меня нет возможности проверить ваши решения
Если слово не написано, то не надо его додумывать.
раскрыть ветку 1 3 года назад Вы слишком мало задачек решали: в 90% случаев задачки заключаются в том, чтобы угадать ответ автора, а не в том что бы решить поставленную задачу 3 года назадА какой вариант решения тут с "только"?
3 года назад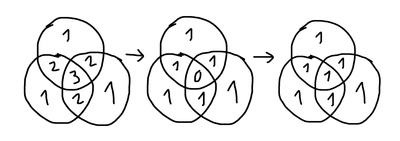
Просто суммируй и отнимай перекрытия, детский сад ё-маё!
Далее в зависимости от того как поняли условие либо три человека помимо учтенных знают языки, либо мы прибавили их 2 лишних раза и нужно отнять 6
77+3 = 80 — 20 человек не знают языков
77-6 = 71 — 29 человек не знают языков
Ждем заёбов от любителей составлять системы уравнений для задач решаемых в уме.
3 года назад раскрыть ветку 2 3 года назад раскрыть ветку 1 3 года назад Точно, с арифметикой совсем туго пол вечер. 3 года назад 20. тремя частично накладывающимися окружностями наглядно получается решить. схему без рейтинга не могу приложить раскрыть ветку 4 3 года назад Приложили уже все равно спасибо) раскрыть ветку 3 3 года назадРешается через формулу включений-исключений одним вычислением:
100 - (30 + 28 + 42) + (8 + 5 + 10) - 3 = 100 - 100 + 23 - 3 = 20.
Чем хороша формула — тем, что подойдёт для любого количества языков, подставь только нужные числа.
раскрыть ветку 2 3 года назад Нам вот таких формул не давали только операции множеств и свойства их. раскрыть ветку 1 3 года назадЗато теперь будете знать :)
3 года назадПервое решение само себе противоречит.
30 = 14 + 5 + 2 + 3 = 24 (?)
Неправильно использована формула включений-исключений.
Правильно (чередуются знаки):
3 года назад Английский - х, немецкий - у, француский - z. Итого простые уравнения с тремя переменными. 3 года назад раскрыть ветку 1 3 года назадВы не отсекли тех кто одновременно владеет 2мя языками?
3 года назад По моему очевидно: 77 3 года назад 30 + 28 + 42 = 100Нет людей не знающих хоть 1 языка раскрыть ветку 1 3 года назад А еще множества могут пересекаться, а не только быть независимыми 3 года назад
Алё! Через систему уравнений и три переменные не проще решить?
раскрыть ветку 3 3 года назад С пересекающимися множествами?Какие переменные вы предлагаете? раскрыть ветку 1 3 года назад 3 года назад
Задача в теме множеств
3 года назадНесколько якорей суммарно весят 10 тонн, причем каждый из них весит не более одной тонны.
Сколько фур-трехтонок заведомо достаточно, чтобы увезти этот груз?
раскрыть ветку 1 3 года назадискал подвох - не нашел. 4?)
показать ещё 0 комментариев Похожие посты 7 месяцев назадЗадача из темы множества. Вам не кажется, что вопрос идиотский?
"Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?"
Здесь же русским языком написано, что 30 -нем. , 28 - анг. , 42- фра., если всех сложить, то получится 30+28+42=100 сто, как раз
Тогда какого хрена спрашивают "сколько туристов не владеют ни одним языком?" ?? ведь из условий получается, что каждый владеет каким-нибудь языком
Тестирование (курильщика)


Было время, когда я тоже жил в Миассе и занимался школьной математикой, весьма неплохо, надо сказать. Поэтому мимо такого поста я не мог пройти. Так бомбануло, что не дочитал, и стал писать ответный с телефона.
Честно говоря, никогда не слышал про эту женщину, пока учился. Но это неважно.
Что важно - это безграмотность журналистов, или кто там текст писал. Статья написана в стиле "срыва покровов": бедную женщину все выпинывают, не хотят даже ковыряться в решении, а ее нужно номинировать на нобелевку.
Даже не смотря на доказательство, уже хочется закрыть статью. Начнем с того, что Нобелевки по математике нет и никогда не было. Продолжим тем, что учительница на пенсии могла потерять хватку в математике, и если она не показала свои результаты коллегам прежде, чем бегать по верхушкам математического мира, то могла упустить существенные вещи. А сильным математикам обычно интересны вопросы посложнее школьной математики, и не надо их винить, что им не очень-то интересна школьная и давно разобранная задача. Закончим отвратительной подачей, которая НАМЕКАЕТ, что здесь МОЖЕТ БЫТЬ что-то интересное, а ученые СКРЫВАЮТ ПРАВДУ, потому что они погрязли в своей теореме невозможности, а она имеет НЕЗАШОРЕННЫЙ ОТКРЫТЫЙ К НОВОМУ УМ. А, ну и ДЕТИ СЕЙЧАС ТУПЫЕ.
Ну что же. Пошевелим остатками мат. знаний в голове и разберём, в чем же проблема. Как по мне, ее мог бы понять любой хороший школьник.
Простейший метод доказательства - пример. И никаких компьютеров не надо, как некоторые уже начали делать. Пишу с телефона, поэтому визуализируйте на листочке.
(Здесь начинается скучная часть)
Итак, берём окружность с центром О. Строим горизонтальный диаметр АВ. Угол АОВ - развернутый, то есть, равен 180 градусов. Трисекция предполагает разбиение на углы по 60 градусов. Итак, строим диаметр CD, перпендикулярный первому. Угол ACB - прямой (вписанный угол равен половине центрального - школьная теорема, есть даже в ЕГЭ), причем СО - биссектриса. На продолжении СО отложим ещё один радиус EC. Получили треугольник АЕВ, угол которого должен быть 60 градусов, да? По построению АЕВ - равносторонний. Но АЕ=ЕВ= корень из 5 радиусов (теорема Пифагора, тоже школьная), АВ - диаметр и равен 2 радиуса. Противоречие.
Почему пенсионерке могло показаться, что она нашла решение? Банальная математическая проблема - неудачный пример.
Попробуем решить в общем виде. Возьмем произвольную хорду АВ окружности, получим произвольный центральный угол АОВ. Построим перпендикулярный диаметр CD и назовем точку пересечения АВ и CD как Н. На продолжении CD отложим радиус ЕС. Угол АЕВ есть два угла АЕН. Пусть заданный угол АОВ равен а, а радиус - р. Тогда тангенс АЕН равен р*sin(a/2)/(2р+р*cos (a/2)) =sin (a/2)/(2+cos (a/2))=tg(a/2)*[cos (a/2)/(2+cos(a/2))]
Копаем глубже: приближенные вычисления для получившегося числа. cos (a/2) приближается к 1 при малых углах. Значит, дробь в квадратных скобках ПРИБЛИЖАЕТСЯ к 1/3. При малых углах (обычно меньше 10 градусов) тангенс ПРИМЕРНО равен самому углу (здесь необходимо уточнить, что это только для углов в радианах, но сути не меняет.). Значит, выражение дает нам ПРИМЕРНО а/6, если считать в радианах. Тогда угол АЕВ ПРИМЕРНО равен а/3, и погрешность тем меньше, чем меньше взят угол.
Понимаете? ВИЗУАЛЬНО эффект будет хороший даже для достаточно больших углов. Я провел вычисления для угла а=60 градусов (примерно тот, что у женщины на картинке) и получил угол при "трисекции", равный 19.79 градусов. Это очень близко к предполагаемым 20.
Какой можно сделать вывод? Если вы нашли простой способ решения нерешенной проблемы - вероятно, он не работает. Десятки людей до вас шли тем же путем, вы вряд ли уникум. Научитесь нормально проверять решение, включая крайние случаи, и тогда одной теорией заговора наверняка станет меньше.
Круги Эйлера, 1 часть, 6 класс

Разработка некоторых материалов (презентации, конспекты) к курсу внеурочной деятельности "Занимательная математика".
Просмотр содержимого документа
«Круги Эйлера, 1 часть, 6 класс»


Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским – 28, французским – 42. Английским и немецким одновременно владеют 8 человек, английским и французским -10 , немецким и французским – 5, всеми тремя языками – 3.
Сколько туристов не владеют ни одним языком?
Выразим условие задачи графически. Обозначим кругом тех, кто знает английский, другим кругом – тех, кто знает французский, и третьим кругом – тех, кто знают немецкий.
французский
Всеми тремя языками владеют три туриста, значит, в общей части кругов вписываем число 3.
французский
Английским и французским языками владеют 10 человек, а 3 из них владеют ещё и немецким. Значит, английским и французским владеют 10-3=7 человек.
В общую часть английского и французского кругов вписываем цифру 7 .
В общую часть английского и немецкого кругов вписываем число 5.
Немецким и французским языками владеют 5 человек, а 3 из них владеют ещё и английским. Значит, немецким и французским владеют 5-3=2 человека.
французский
В общую часть немецкого и французского кругов вписываем цифру 2.
Известно, что немецким языком владеют 30 человек, но 5+3+2=10 из них владеют и другими языками, значит, только немецкий знают 20 человек.
Ответ: 20 человек.

Рисунки, подобные тем, что мы рисовали при решении этой задачи, называются «кругами Эйлера». Один из величайших математиков Петербургской академии Леонард Эйлер написал более 850 научных работ. В одной из них и появились эти круги. Эйлер писал тогда, что «они очень подходят для того, чтобы облегчить наши размышления». Наряду с кругами в подобных задачах применяют прямоугольники и другие фигуры.

Леонард Эйлер (15 апреля 1707 г. – 18 сентября 1783 г.)
Учить всему надо легко, доступно и наглядно.
Леонард Эйлер
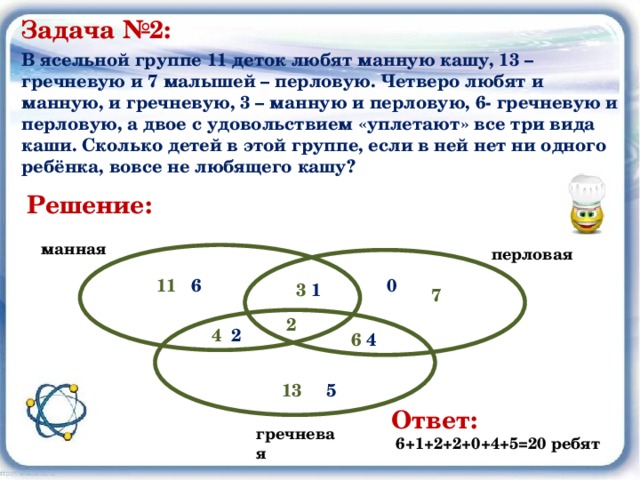
В ясельной группе 11 деток любят манную кашу, 13 – гречневую и 7 малышей – перловую. Четверо любят и манную, и гречневую, 3 – манную и перловую, 6- гречневую и перловую, а двое с удовольствием «уплетают» все три вида каши. Сколько детей в этой группе, если в ней нет ни одного ребёнка, вовсе не любящего кашу?
Правило Гаусса, история появления
Жил-был маленький Гаусс. Ходил он ещё в начальную школу. А учителей уже тогда не хватало, поэтому малышня из начальных классов вполне могла сидеть на одном уроке в одном классе с ребятами из средних. Учитель математики, который был явно не в восторге от таких двойных уроков, самым маленьким дал задание : подсчитать сумму всех чисел от одного до ста. И они на грифельных досках пошли старательно считать. А преподаватель занялся ребятами из среднего класса. К концу урока стал проверять, что же у кого получилось. Результата правильного не было ни у кого. Только у Гаусса не было вычислений и в ответе стояла правильная цифра 5050.
- Кто тебе подсказал, признавайся!
- Никто, это я сам.
Учитель не поверил. Тогда маленький мальчик пояснил ход своих рассуждений. Он сложил 1+100=101. Затем 2+99=101. И так 50 раз. Тогда 101*50=5050. Остальные ученики в жару творческого порыва просто складывали последовательно 1+2+3+4 и так далее. И в их вычисления неизбежно закрадывалась ошибка.
Смотреть нетривиально на поставленные задачи и включать голову могут не все. Лишь некоторые. И вот они как раз и двигают прогресс.

Ответ на пост «Домашнее задание семилетнего ребенка поставило в тупик доктора наук»
Вспомнилось моё школьное задание по физике: определить размер молекулы растительного масла.
Было ещё во времена СССР. Уроки по физике, 6-ой класс. Сразу же после темы о молекулах и атомах учитель даёт нам задание до следующего занятия экспериментально определить размер молекулы растительного масла.
Я не знаю как, родители тоже - они в недоумении. На следующем занятии, как оказалось, никто не смог измерить. Но учитель и не настаивал, просто перешёл к другим темам.
Спустя несколько лет, уже учась в серьёзном техническом ВУЗе, на вечере выпускников я вспомнил тот случай и спросил учителя о сути того задания.
Он ответил, что это была проверка, так сказать, на вундеркиндость.
Типа надо было взять маленькую каплю масла и капнуть на поверхность воды. Масло бы растеклось, образуя плёнку. И, зная объём капли и диаметр плёнки, через несложные формулы можно было бы рассчитать толщину плёнки, которая и равна размеру молекул.
Я промолчал, но подумал, что физик-то совсем не того, потому что:
1. Растительное масло состоит из кучи веществ и нет такого понятия как "молекула растительного масла";
2. Почему-то учитель считал, что образуется плёнка толщиной в одну молекулу, что совсем не так.
Но, наверное, ему был важен подход, а не результат. И среди нас, к сожалению, вундеркиндов не нашлось.
Показать полностью 7 месяцев назадПомогите пожалуйста, информатика 7 класс.
1. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?
2. . Из 50 участников олимпиады по информатике, первую задачу решило 25 человек, вторую - 24, третью - 21. Первую и вторую задачи решило 9 человек, вторую и третью - 10, первую и третью – 12 человек, все три задачи - 8. Сколько участников не решили ни одной задачи?
Задачи на круги Эйлера
Очень часто бывает так, что решение задачи помогает найти рисунок. Использование рисунка делает решение задачи простым и наглядным .
Рассмотрим такую задачу.
1). В классе 35 учеников. Из них: 19 ребят занимают в математическом кружке, 10 - в биологическом, 9 ребят не посещают эти кружки. Сколько биологов увлекаются математикой?
Решение. Для решения задачи изобразим в виде "кругов" учащихся,
занимающихся математикой и биологией.
Обозначим их буквами М и Б соответственно. Круги М и Б содержатся в прямоугольнике, которым мы изображаем всех учащихся класса.

Нам очевидно, что общая часть кругов М и Б состоит из тех ребят, которые одновременно увлекаются и математикой, и биологией. Теперь давайте посчитаем. Всего внутри прямоугольника 35 ребят. Внутри двух маленьких кругов М и Б будет 35-9= 26 ребят, поскольку нам известно, что 9 ребят не посещают кружки. Внутри "математического" круга 19 ребят, значит, в той части "биологического" круга, которая расположена вне круга М, находится 26-19= 7 биологов, не посещающих математический кружок. Остальные биологи, их 10-7= 3, находятся в общей части кругов МБ. Таким образом, 3 биолога увлекаются математикой.
Изображение различных множеств в виде кругов широко использовал в своих научных трудах великий математик Х VIII века Леонард Эйлер. Именно поэтому рисунки, подобные в задаче, которую разобрали выше, обычно называют "кругами Эйлера". Эйлер отмечал, что изображение множеств в виде кругов "очень подходит для того, чтобы облегчить наши рассуждения".
Круги Эйлера - геометрическая схема, с помощью которой можно изобразить отношения между подмножествами.
2). В киоске около школы продается мороженое двух видов: "Спортивное" и "Мальвина". На перемене 24 ученика успели купить мороженое. При этом 15 из них купили "Спортивное", а 17 - мороженое "Мальвина". Сколько человек купили мороженое обоих сортов?
Решение. Попробуем изобразить данные задачи с помощью кругов.
Общая часть кругов состоит из тех школьников, которые купили мороженое обоих сортов. Всего мороженое купили 24 ученика. Внутри круга М 17 учеников, а в круге С - 15 учеников. Возьмем, например, учащихся, купивших мороженое "Мальвина". Получим 24-17=7 учащихся, которые купили мороженое "Спортивное", но не купили мороженое "Мальвина". Остальные учащиеся: 15-7= 5 купили и мороженое "Спортивное", и "Мальвина". Таким образом, мы получили 5 учеников, которые купили оба вида мороженого.
3). Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?
Ответ: только английским владеет 13 человек, только французским - 30, только немецким - 20 человек.20 человек не знают ни одного из этих языков.
4). В классе 30 человек.20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуется всеми тремя видами транспорта?
Решение: Для решения опять воспользуемся кругами Эйлера.
Пусть х - человек пользуется всеми тремя видами транспорта. Тогда пользуются только метро и троллейбусом - (10 − х) человек, только автобусом и троллейбусом - (9 − х) человек, только метро и автобусом - (12 − х) человек. Найдем, сколько человек пользуется одним только метро: 20 − (12 − х) − (10 − х) − х = х − 2. Аналогично получаем: х − 6 - только автобусом и х + 4 - только троллейбусом, так как всего 30 человек, составляем уравнение: х + (12 − х) + (9 − х) + (10 − х) + (х + 4) + (х − 2) + (х − 6) = 30, отсюда х = 3.
Задачи для самостоятельного решения:
1) В трех шестых классах 70 ребят. Из них 28 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке 10 ребят из хора, в хоре 6 спортсменов, в драмкружке 8 спортсменов, 3 спортсмена посещают и драмкружок и хор. Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке? Сколько ребят заняты только спортом?
2) В классе 38 человек. Из них 16 играют в баскетбол, 17 - в хоккей, 18 - в футбол. Увлекаются двумя видами спорта - баскетболом и хоккеем - четверо, баскетболом и футболом - трое, футболом и хоккеем - пятеро. Трое не увлекаются ни баскетболом, ни хоккеем, ни футболом, а 2 школьника увлекаются сразу тремя видами спорта. Сколько ребят увлекается лишь одним из этих видов спорта?
3). Из 100 человек 85 знают английский язык.80 - испанский, 75 - немецкий. Сколько человек знают только один язык, если все три знают 10 человек?
4). В классе 30 человек.20 из них каждый день пользуются метро, 15 - автобусом, 23 - троллейбусом, 10 - и метро, и троллейбусом, 12 - и метро, и автобусом, 9 - и троллейбусом, и автобусом. Сколько человек ежедневно пользуются всеми тремя видами транспорта?
5). Контрольная работа по математике состояла из задачи, уравнения и неравенства. Контрольную работу писали 40 человек. Правильно решили только задачу 2 ученика, только неравенство - 4 человека, только уравнение - 3 человека. Не решили только задачу 7 человек, только уравнение - 5 человек, только пример - 6 человек. Остальные выполнили всю работу правильно. Сколько таких учащихся ?
5. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. Английским и немецким одновременно владеют 8 человек, английским и французским - 10, немецким и французским - 5, всеми тремя языками - 3. Сколько туристов не владеют ни одним языком?
Найди верный ответ на вопрос ✅ «5. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42. . » по предмету 📙 Математика, а если ответа нет или никто не дал верного ответа, то воспользуйся поиском и попробуй найти ответ среди похожих вопросов.
Новые вопросы по математике
2 тыс=. Дес 2 дес. тыс.=тысяч. 5 сот тысяч=дес. тыс 3 дес. тыс=сот тысяч 10 дес=ед 20 дес. тыс=сот тысяч
Рівняння 14010 - z = 3815
В треугольнике авс сторона ав=корень из 43, вс=корень из 59, ас=4. Найдите величину наибольшего угла
Сколько существует различных расположений 15 монеток, в которых нет 2 подряд идущих орлов?
Стороны треугольника равны 3/8 м, 1/2 м, 5/6 м. найти периметр
Главная » ⭐️ Математика » 5. Из 100 туристов, отправляющихся в заграничное путешествие, немецким языком владеют 30 человек, английским - 28, французским - 42.
Читайте также:


