Несколько мальчиков встретились на вокзале чтобы поехать за город в лес
Задача 3. Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?
Слайд 10 из презентации «Применение теории графов к решению задач»
Друзья встретились на остановке, чтобы поехать на футбольный матч. При встрече все они поздоровались друг с другом за руку. Сколько было мальчиков, если в его было 15 рукопожатий

Всего было 6 мальчиков. 5 рукопожатий (1 мальчик с остальными пяти) + 4 рукопожатия (еще один мальчик с другими, т.к. второй раз он не будет с одним и тем же здороваться) + 3 + 2 + 1 = 15 рукопожатий.
Новые вопросы в Математика
Выделать квадрат двучлена
Наити сумму чисел 7 и6, 8 и5, 9и 3
Как сделать пример 30×31 быстро
201. На рисунке 1.24 изображен прямоугольник длиной 10 см, шириной 5 см. Найдите площадь закрашен- ной части прямоугольника.
(270000+80000)÷1000÷7=?
Як на координатному промені розміщена точка з меншою координатою відносно точки з більшою координатою?
1 000 000 – 62 ·X = 987 600пожалуйста помогитедам 14 баллов
срочно пж пж пж пж пж пж
Сократи дробь (Между числом и переменной пробел не вставлять!): 6dnm ---------= 27dmt помогите даю 15 баллов!
Постройте диаграмму. Масштаб: 1 клеточка = 30 предметов. ЗАДАЧА ТАКАЯ На клумбе росло 240 ромашек, тюльпанов — на 150 меньше, а фиалок— в 3 раза больш … е, чем тюльпанов. Сколько фиалок росло на клумбе? Я ЕЕ РЕШИЛА НО МОГУ РЕШИТЬ 2 ВАРИАНТ ПОМОГИТЕ ПОЖАЛУЙСТА
Помогите пожалуйста с 552

Около дома (словоформа), смешной мальчишка (словосочетание), закадычный друг (фразеологический оборот), играть в мяч (словосочетание), мимо ворот (словоформа), игра продолжается (сочетание подлежащего и сказуемого), бежать по полю (словосочетание), громко смеяться (словосочетание), бить баклуши (фразеологический оборот), прилетели птицы (сочетание подлежащего и сказуемого), в течение года (словоформа).
Новые вопросы в Русский язык
помогите с русским!!
Помоги мне. Срочно сейчас же!
Опишите один из портретов художников («Джоконда» Леонардо да Винчи. «Незнакомка» Крамского. « Пушкин» О. Кипренского и т.п.) Используйте в работе порт … ретную лексику. Обратите внимание: художник, в отличие от фотографа, стремится изобразить самое существенное в человеке; в работе важно не перечисление всех компонентов портрета, а умение уловить, что характерно для данного человека, составляет его индивидуальность, главное в нем. В связи с этим текст, содержащий описание портрета, обладает следующими структурно – композиционными особенностями: общая характеристика, история создание портрета; собственно портрет – внешние данные (лицо, глаза, волосы, одежда); особенности душевного состояния, характера, отраженные в портрете; оценка портрета. Глаза – серые, карие, синие, черные, зеленые, голубые, темные, светлые, добрые, узкие, большие, раскосые, хитрые, со смешинкой, дикие, приветливые, серьезные, задумчивые, мутные, холодные, выразительные, тусклые, продолговатые и т.д. Нос – прямой, с горбинкой, горбатый, курносый, вздернутый, широкий, узкий, острый и т.д. Лицо – овальное, круглое, вытянутое, открытое, гладкое, подвижное, смуглое, бледное; черты лица – выразительные, мелкие, крупные, резкие, красивые, мягкие и т.д. Волосы – каштановые, светлые, русые, густые, пышные, короткие, длинные, прямые, волнистые, кудрявые, торчащие, взъерошенные, прилизанные, рыжие, пепельные, распушенные и т.д. Улыбка – милая, злая, презрительная, веселая, вымученная, приветливая, насмешливая, очаровательная, жалкая, кривая, лукавая, счастливая, слабая и т.д.
1) укажите словосочетание со связью управление впервые поразился, однажды смотрел открой книгу по настоящему взволнован. 2)выпишете грамматическую осн … ову предложения зелень сохранила свою свежесть да начала июля вследствие того что весна была сырая
1)Найдите ряд, в котором сочетания слов не являются словосочетаниями. 1 солнце встает, около пруда, пить и есть 2 пребывать в городе, жёлтый цыпленок … , острый циркуль 3 яркий свет, очень быстро, цвет хаки 4 долго идти, масляные краски, сидеть на террасе 2)Продолжите высказывание, запишите пропущенное слово. В словосочетании «её глаза» способ подчинительной связи – ________. 3)Найдите ряд, в котором все словосочетания именные. очень приятно, слева от нас пять подруг, кто-то из друзей далеко от дома, подойти к тропе вспоминая о прошлом, внимательно слушающий 4)Укажите тип подчинительной связи в словосочетании «по-осеннему холодно». управление согласование примыкание это не словосочетание, поэтому тип связи определить нельзя
Помогите пожалуйста. Продолжите предложение так, чтобы получилось сложносочинённое. Стояла необычайно тёплая осенняя погода …А удивлявшая даже старико … в Б когда солнце греет жарче, чем летом В и на пляже, словно летом, было много отдыхающих Г солнце грело жарче, чем летом
Напишите пожалуйста сочинение по произведению Шишкина «на севере диком» и а начале немного биографии о его творчестве
ПОМОГИТЕ ПОЖАЛУЙСТА. СРОЧНО. дам 15 балловПрочитайте текст и выполните задания (только 2 и 3) ТЕКСТ:В творчестве художника И. И. Шишкина очевидно … стремление создать обобщённый образ роднои природы воспеть ее неподвластную времени красоту и величие. в картине «Рожь» (1878) присутствует ряд элементов, ха рактеризующих национальный пейзаж: уходящая вдал, дорога, золотое поле созревающей ржи и высокие, прямые сосны, тянущиеся к небу, Мы видим ломкие стебли ко- лосьев, лопушки на дороге и даже тень под брюшком стре- мительно пролетающего низко над землёй стрижа. В глу. бине композиции мелькают яркие платки идущих по полю крестьянок. Духота жаркого дня передаётся горячим золотистых цветом ржаного поля и неподвижностью застывших в про- странстве сосен. едва уловимая взглядом. Тяжёлые колосья, пригибаемые ветром, ложатся на землю. Шелестит ржаное море, колеб- лемое ветром. Чьи-то голоса, слышимые издалека, гулко раздаются среди шелеста трав. Вдали темнеет почти не- видимый лес. Могучие сосны, согреваемые солнцем, тя- нутся к небу. Облака, движимые из-за горизонта порыва- ми ветра, клубятся в полупрозрачной синеве неба.Задания приклеплю на фото
Даю 35 баллов тому кто поможет с сочинением . В эссе дайте развёрнутый ответ (12-15 предложений) на эти вопросы, приведите аргументы, сделайте вывод … Мы часто повторяем, что о человеке судят по делам его, но забываем, что слово тоже поступок. Речь человека - зеркала его самого эссе.
Похожие презентации
краткое содержание других презентаций на тему слайда«Социальные отношения» - Социальные отношения. Эргономика. Политология. Формационный подход. Предприятие. Духовная сфера. Структура социоэкономических отношений. Семья. Историческая форма социально-экономических отношений. Вариант 1. СЭО доиндустриального общества. Формы институционализации СЭ. Социально- политические отношения.
«Спрос и цена» - Ограниченный ресурс. Задание для учащихся. Институт частной собственности поддерживается правом завещания. Рыночная экономика. КОНКУРЕНЦИЯ ( competition)- борьба за наиболее выгодные условия производства и сбыта товаров. Потребительский выбор определяет что будет производить производитель. Вопросы для обсуждения.
«Кейнсианская и классическая теория» - Денежная масса. Роль государства. Государство поддерживает денежную массу. Рынок капитала. Рынки труда и потребительских товаров. ВВП. Рынок труда и потребительских товаров. Неоклассическая теория. Рынок денег. Основные идеи кейнсианства. Рынок потребительских товаров. Рыночная экономика. Основные идеи неоклассицизма.
«Факторы производства» - Менеджмент. Основные факторы производства. Ресурсы существуют независимо друг от друга. Ресурсы. Производство. Капитал. Факторные доходы. Факторы производства подвластны действию закона. Факторы производства. Денежные средства. Маркетинг. Управление. Ресурсы, вовлеченные в процесс производства. Что такое факторы производства.
«Правила и институты» - Неформальные институты вытесняют формальные. Эггертссон Т. Экономическое поведение и институты. Дополнительная литература. 1.3. Правила. Все вокруг – институциональная экономика. Правила. Зачем Сталину были нужны массовые репрессии? Перечень правомочий по оноре. c. Ограниченная рациональность – следствие ограниченности познавательных способностей индивидов.
«Экономическая теория» - Проблема выбора. Наука, изучающая способы удовлетворения потребностей. Двумерная экономическая модель. Место экономической теории. Система хозяйствования. Закон возрастания альтернативной стоимости. Производственные возможности. Блага. Экономика как учебная дисциплина. Основные понятия. Предмет и метод экономической теории.
"Семинар ДООМ" Решение логических задач с помощью графов.
Тема урока: «Решение логических задач с помощью графов».
Цель: Ввести понятие «графа», научить решать логические задачи с помощью графа.
1. Изучение темы полезно начать с решения конкретной задачи: Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий? Будем решать эту задачу графически. Вначале отметим точки А и В и соединим их отрезком. Точками будем изображать мальчиков, а отрезок будет означать рукопожатие. Добавим еще одну точку С и соединим её с точками А и В. Всего получается три отрезка.
Отметим следующую точку Д и соединим её отрезками с тремя точками А, В и С. Теперь уже получилось шесть отрезков. Наконец, отметим пятую точку Е и соединим её со всеми точками, отмеченными ранее. Получилось 10 отрезков, т. е 10 рукопожатий. Значит, на вокзале встретились 5 мальчиков. (Так как урок проходит в 6 классе, то можно проводить его с элементами игры, т. е. предложить ребятам проверить решение на практике. Вызвать к доске сначала 2, затем 3, 4 и 5 учащихся и попросить их пожать друг другу руки. Весь класс сможет убедиться, что всего было 10 рукопожатий.)

Графы помогают решать некоторые задачи. Разберем одну из них.
Решение. Здесь мы имеем два равночисленных множества: множество фамилий и множество цветов платьев. Между этими множествами надо установить взаимно-однозначное соответствие. Для этого построим граф. Пусть белые кружочки Б, К и Ч изображают элементы первого множества (Белова, Краснова и Чернова), а черные кружочки б, к и ч – элементы второго множества – белое, красное и чёрное. Условимся соединять эти кружочки тонкой линией, если между ними нет соответствия. Если же соответствие между кружочками установлено правильно, то будем соединять их жирной линией.
Следовательно, Белова одета в чёрное платье, Чернова одета в красное платье и Краснова – в белое платье.
Теперь видно, что долететь от Земли до Марса нельзя. Задача 2. Петя, Гена, Дима и Вова занимаются в детской спортивной школе в разных секциях: гимнастической, баскетбольной, волейбольной и легкой атлетики. Петя, Дима и волейболист учатся в одном классе. Петя и Гена на тренировки ходят пешком вместе, а гимнаст ездит на автобусе. Легкоатлет не знаком ни с баскетболистом, ни с волейболистом. Кто из мальчиков в какой секции занимается? Решение. Петя – баскетболист, Гена – волейболист, Дима – гимнаст, а Вова – легкоатлет.
3. Для закрепления изученного материала можно решить устно № 1220 (а) ( стр. 210, учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005.)
Ответ: Витя знаком с Серёжей и Колей, Серёжа знаком с Витей и с Пете, Петя знаком с Серёжей и с Максимом, Максим знаком с Пете и с Колей, Коля знаком с Петей и с Витей.
4. Домашнее задание. № 1249, № 1303. (учебник «Математика 6», автор Н.Я. Виленкин, М.: Мнемозина, 2005)
№ 1249. Вера, Нина, Оля и Люба надели платья разных цветов (красное, синее, белое, голубое). На вопрос, кто из них в каком платье, три девочки ответили: 1) Оля – в синем. Люба – в голубом; 2) Оля – в красном. Нина – в синем; 3) Вера – в синем, Люба – в голубом. В каждом ответе только одна часть верна, а другая нет. Какого цвета платье надела каждая девочка?
№ 1303. Марина, Лариса, Жанна и катя умеют играть на разных инструментах (пианино, виолончели, гитаре, скрипке), но только каждая на одном. Они же знают иностранные языки (английский, французский, немецкий. Испанский), но каждая только один. Известно: 1) девушка, которая играет на гитаре, говорит по-испански; 2) Лариса не играет ни на скрипке, ни на виолончели и на знает английского языка; 3) Марина не играет ни на скрипке, ни на виолончели и на знает ни немецкого, ни английского языка; 4) девушка, которая говорит по-немецки, не играет на виолончели; 5) Жанна знает французский язык, но не играет на скрипке. Кто на каком инструменте играет и какой иностранный язык знает?
Предварительный просмотр:
Решите логические задачи
1.Игорь, Петя и Саша ловили рыбу. Каждый из них поймал либо ершей, либо пескарей, либо окуней.
Кто из них каких поймал рыб,
если известно, что:
- Колючие плавники есть у окуней и ершей, а у пескарей их нет;
- Игорь не поймал ни одной рыбы с колючими плавниками;
- Петя поймал на 2 окуня больше, чем поймал рыб Игорь?
Сколько рыб поймал каждый из мальчиков, если Игорь поймал 3 рыбы, а всего рыб было меньше 10?
2.В одном доме живут Воронов, Павлов, Журавлев, Синицын. Один из них математик, другой – художник, третий – писатель, а четвертый – баянист. Известно, что: ни Воронов, ни Журавлев не умеют играть на баяне; Журавлев не знаком с Вороновым; писатель и художник в воскресенье уезжают на дачу к Павлову; писатель собирается написать очерк о Синицыне и Воронове. Требуется определить, кто есть кто.
3. Несколько мальчиков встретилось на вокзале, чтобы поехать в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было 10 рукопожатий?
4. Три друга – Алеша, Сережа и Денис – купили щенков разной породы – колли, ротвейлер и овчарку – и дали им клички – Лесси, Джек и Гриф. Известно, что щенок Алеши темнее по окраске, чем овчарка, Лесси и Джек; щенок Сережи старше Джека, ротвейлера и овчарки. Какой породы щенок и с какой кличкой у каждого из ребят? Технология решения:
- В один столбец записывают одни данные, а в другой – другие.
- Рассуждают и об истинности ложности предположений.
- Если предположение истинно, то значение столбиков соединяется сплошной стрелочкой, а если ложное, то пунктирной стрелочкой.
- В результате должен получиться правильный ответ.
5. В классе 36 человек. Ученики этого класса посещают математический, исторический и географический кружки, причем математический кружок посещают 18 человек, исторический – 14 человек, географический – 10 человек. Кроме того, известно, что 2 человека посещают все три кружка, 8 человек – математический и исторический, 3 – исторический и географический, 5 – математический и географический. Сколько человек из класса не посещают никаких кружков? ( Для решения задач такого типа очень удобным является использование кругов Эйлера. Самый большой круг обозначает множество всех учеников в классе. Внутри этого круга изображаем множества учеников математического, исторического и географического кружков. Заполняя числами, начиная с тройного пересечения, все области пересечений данных окружностей.)
6. Четыре футбольных команды: итальянская команда «Милан», испанская – «Реал», российская – «Зенит», английская – «Челси» встретились в групповом этапе лиги чемпионов по футболу. Их тренировали тренеры из этих же четырех стран: итальянец Антонио, испанец Родриго, русский Николай, англичанин Джон. Известно, что национальность у всех четырех тренеров не совпадала с национальностью команд. Требуется определить тренера каждой команды, если известно: а) «Зенит» не тренируется у Джона и Антонио. б) «Милан» обещал никогда не брать Джона главным тренером.
7. Во дворе дети катались на велосипедах.
Самые маленькие на 3-хколесных. Школьники на 2-хколесных.
Миша сосчитал, что у всех велосипедов было 12 колес.
Сколько на 3-х и 2-х колесных велосипедов было на улице?
8. На трех мешках наклеены надписи : рис, сахар, мука или сахар. Что в каждом мешке, если известно, что все наклейки не верны?
Графы. Схема отношений

В данном проекте учащиеся изучают основные понятия: граф, ориентированный граф, неориентированный граф, схема отношений.
Эта работа также знакомит школьников с областью применения этой темы на других предметах.
В презентацию вставлена практическая работа, которая позволяет закрепить умения изображать графически схему отношений между объектами.
Граф состоит из точек (вершин) и линий (ребер), связывающих точки.
Схема отношений – это граф, вершины которого соответствут объектам, а ребра – отношениям между ними.
Некоторые отношения между объектами описываю с помощью направленных ребер. (Имена отношений изменятся, если два объекта в паре поменять местами.)
Первая работа о графах появилась в 1736 году в публикациях Петербургской академии наук. Она принадлежит Леонарду Эйлеру и связана с решением задачи о Кенигсбергских мостах.
Содержимое разработки

- Что мы понимаем под объектами?
- Можем ли мы города(людей, машины) рассматривать как объекты?
- Как вы понимаете выражение «отношения между объектами»?
ЗАДАЧА
Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехали за город, если всего было 10 рукопожатий?

Графы. Схема отношений.
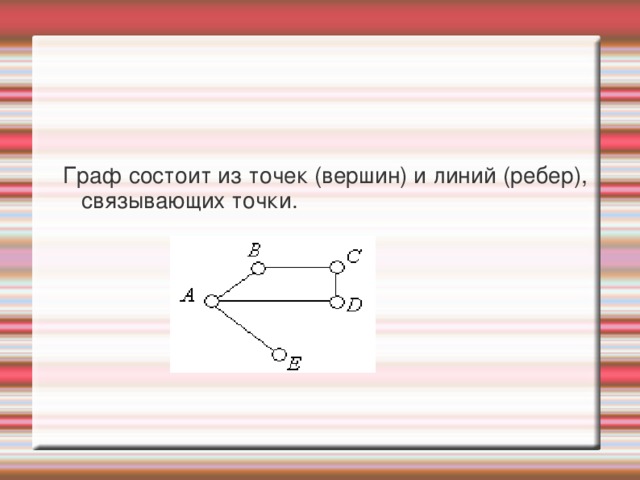
Граф состоит из точек (вершин) и линий (ребер), связывающих точки.
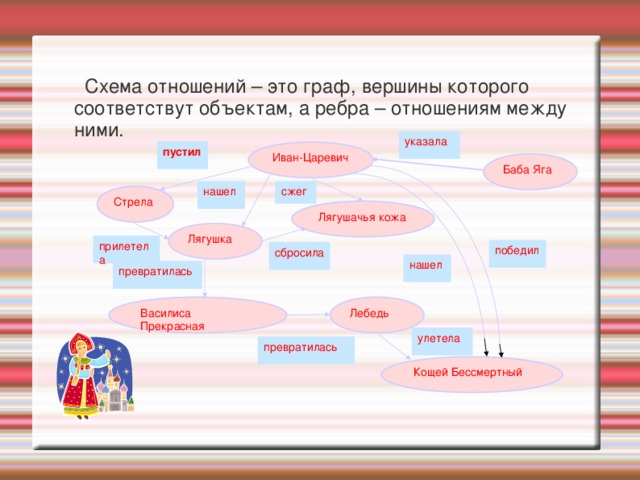
Схема отношений – это граф, вершины которого соответствут объектам, а ребра – отношениям между ними.
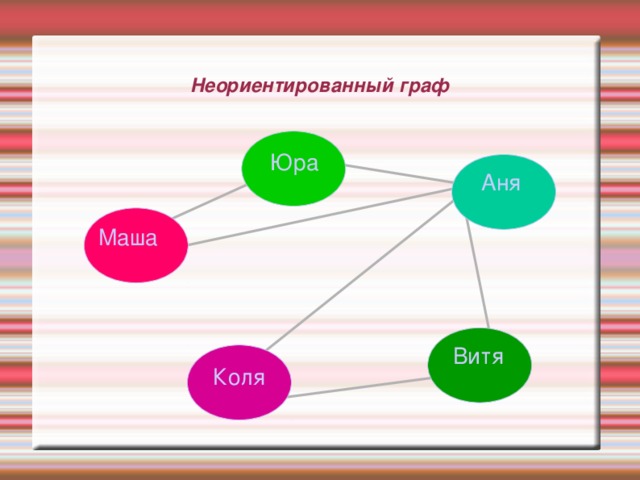
Неориентированный граф
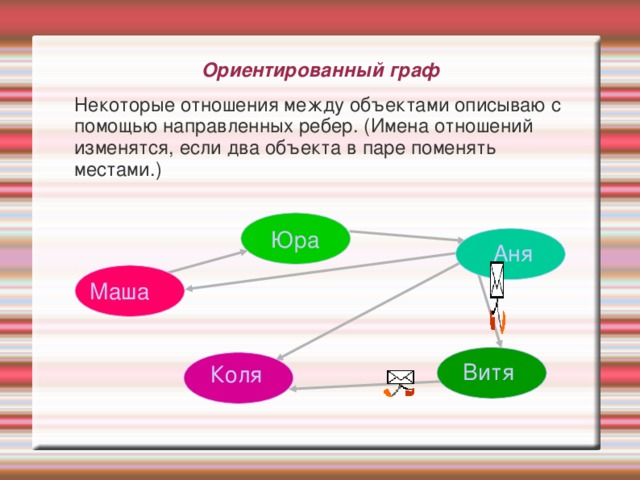
Ориентированный граф
Некоторые отношения между объектами описываю с помощью направленных ребер. (Имена отношений изменятся, если два объекта в паре поменять местами.)

Устная работа стр: 14 задание 8,9
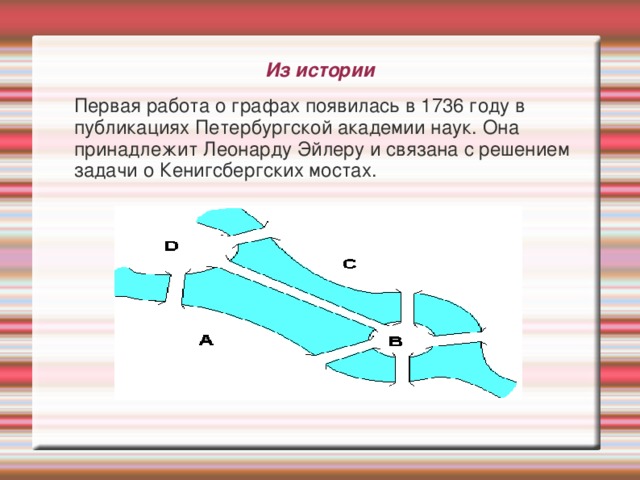
Из истории
Первая работа о графах появилась в 1736 году в публикациях Петербургской академии наук. Она принадлежит Леонарду Эйлеру и связана с решением задачи о Кенигсбергских мостах.



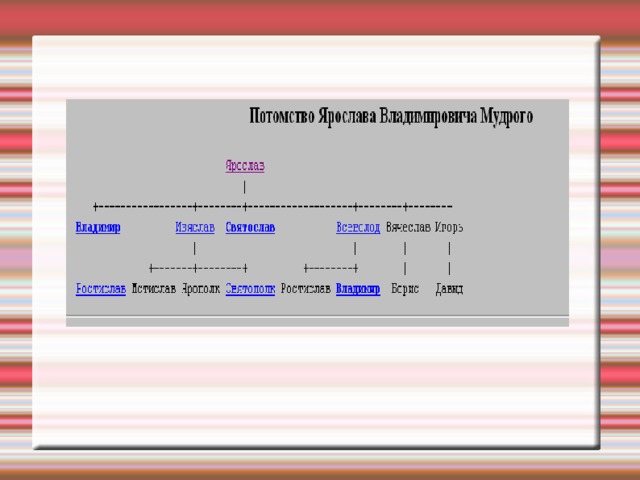

ФИЗМИНУТКА

«Построение схемы отношений между объектами» Цель: научиться строить схему отношений между несколькими объектами с помощью графов.
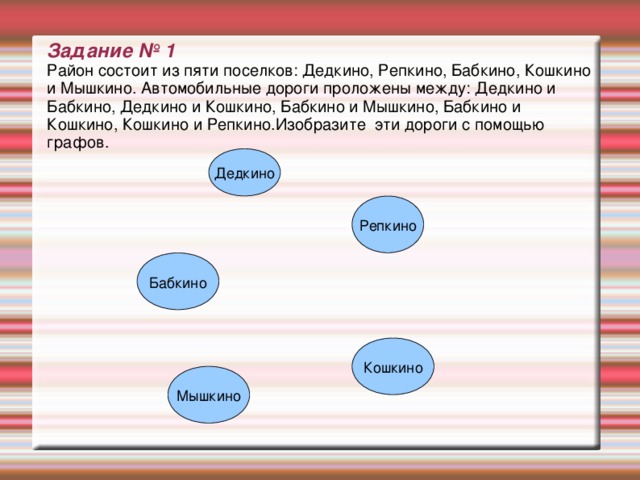
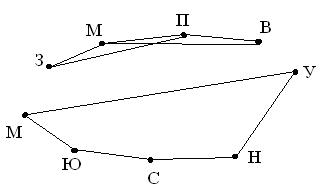
Задание № 1 Район состоит из пяти поселков: Дедкино, Репкино, Бабкино, Кошкино и Мышкино. Автомобильные дороги проложены между: Дедкино и Бабкино, Дедкино и Кошкино, Бабкино и Мышкино, Бабкино и Кошкино, Кошкино и Репкино.Изобразите эти дороги с помощью графов.
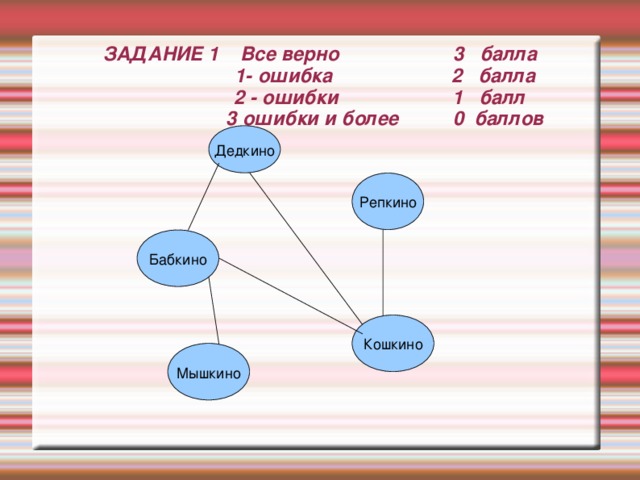
ЗАДАНИЕ 1 Все верно 3 балла 1- ошибка 2 балла 2 - ошибки 1 балл 3 ошибки и более 0 баллов
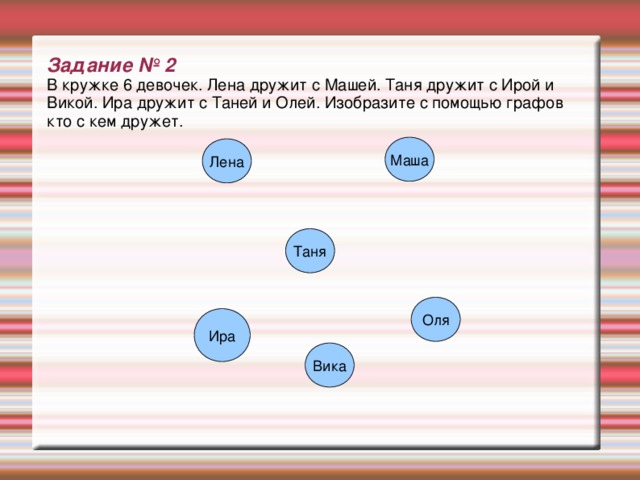
Задание № 2 В кружке 6 девочек. Лена дружит с Машей. Таня дружит с Ирой и Викой. Ира дружит с Таней и Олей. Изобразите с помощью графов кто с кем дружет.
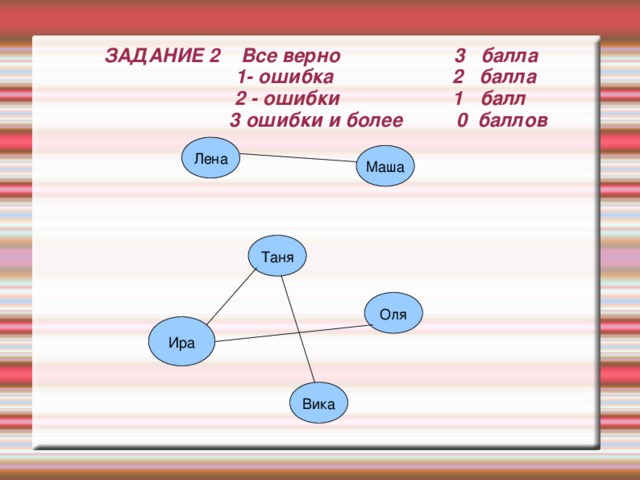
ЗАДАНИЕ 2 Все верно 3 балла 1- ошибка 2 балла 2 - ошибки 1 балл 3 ошибки и более 0 баллов

Задание № 3 В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий? Изобрази условие задачи с помощью графов.. Запиши ответ задачи под рисунком.
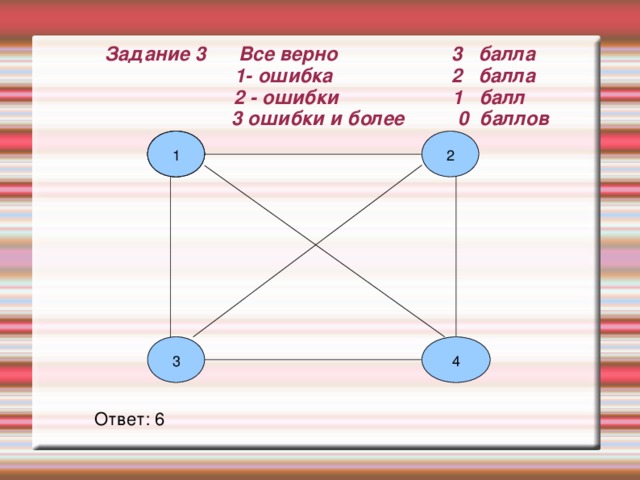
Задание 3 Все верно 3 балла 1- ошибка 2 балла 2 - ошибки 1 балл 3 ошибки и более 0 баллов

Задание № 4 На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Соедини деревья от самого низкого к самому высокому ориентированными графами. Определи какое дерево самый высокое и какое самое маленькое.
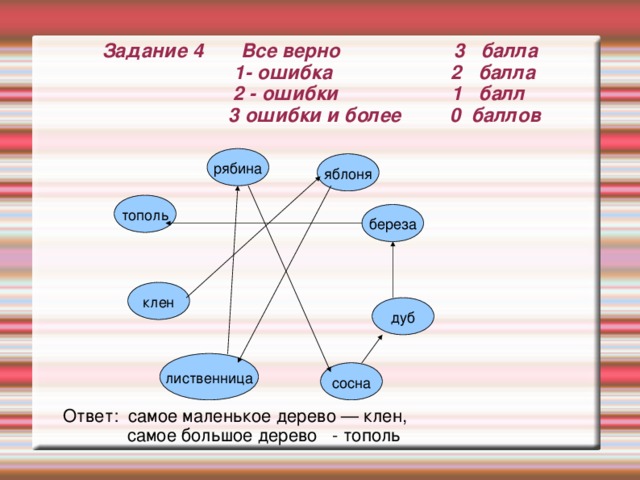
Задание 4 Все верно 3 балла 1- ошибка 2 балла 2 - ошибки 1 балл 3 ошибки и более 0 баллов
Ответ: самое маленькое дерево — клен,
самое большое дерево - тополь
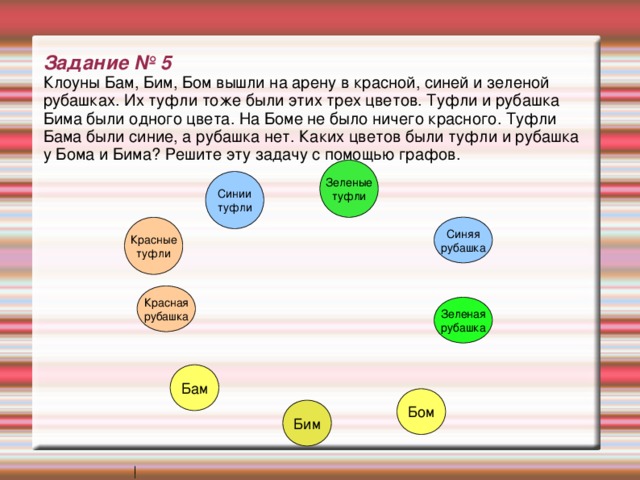
Задание № 5 Клоуны Бам, Бим, Бом вышли на арену в красной, синей и зеленой рубашках. Их туфли тоже были этих трех цветов. Туфли и рубашка Бима были одного цвета. На Боме не было ничего красного. Туфли Бама были синие, а рубашка нет. Каких цветов были туфли и рубашка у Бома и Бима? Решите эту задачу с помощью графов.
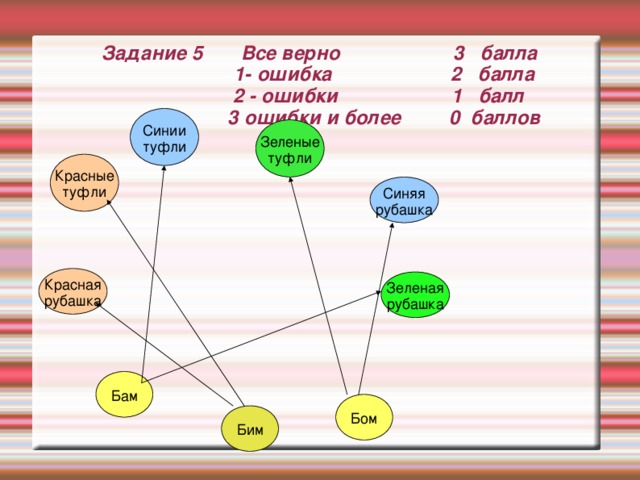
Задание 5 Все верно 3 балла 1- ошибка 2 балла 2 - ошибки 1 балл 3 ошибки и более 0 баллов

Оценки
15 баллов - «5» 14-13 баллов - «4» 12 баллов - «3»

Домашняя работа : изобразить с помощью графов генеалогическое древо своей семьи.

Предварительный просмотр:
Задачи на движение
Машина прошла первый участок пути за 3 часа, а второй участок - за 2 часа. Длина обоих участков вместе 267 км. С какой скоростью шла машина на каждом участке, если скорость на втором участке была на 8,5 км/ч больше, чем на первом? Построим сетевой граф.
Пусть V 1 = х км/ч, тогда V 2 = х+ 8,5 км/ч, S 1 = 3х км, S 2 = 2( х+8.5)км . Составим уравнение: 3х + 2( х+8,5) = 267 Ответ: 50 км/ч
Мотоциклист проехал расстояние от одного города до другого за 3 часа, двигаясь со скоростью 54 км/ч. Сколько времени потребуется мотоциклисту на обратный путь, но уже по другой дороге, если она длиннее первой на 22 км, а его скорость будет меньше прежней на 8 км/ч.
Сетевой граф будет выглядеть следующим образом: S 1 =162 км v 1 =54 км/ч t 1 =3 ч
S 2 = 184 км v 2 = 46 км/ч t 2 = 4 ч
S 1 2 на 22 км v 1 >v 2 на 8 км/ч Ответ: 4 часа.
«Друзья» . В спортивном зале собрались Витя, Коля, Петя, Сережа и Максим. Каждый из мальчиков знаком только с двумя другими.
Кто с кем знаком? Решение: Построим граф.
Ответ: Витя знаком с Колей и Сережей, Сережа с Витей и Петей, Петя с Сережей и Максимом, Максим с Петей и Колей, Коля с Петей и Максимом.
«Туристы» Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехали за город, если всего было 10 рукопожатий?
Решение. Сделаем рисунок. Точки будут изображать мальчиков, а отрезки рукопожатия Ответ: 5
Школа диалога культур «МОСТ»
«Ещё один способ решения задач»
Автор: Пыркова Мария,
обучающаяся 7 класса
школы-интерната № 9 ОАО
«РЖД» г.Кинель Самарской
Степанова Ольга Алексеевна,
учитель математики высшей категории.
« Рано или поздно всякая правильная математическая идея находит применение в том или ином деле». (А.Н. Крылов)
Слово «граф» в математике означает картинку, где нарисовано несколько точек, некоторые из которых соединены линиями. Графами являются блок – схемы программ для ЭВМ, сетевые графики строительства, где вершины – события, означающие окончания работ на некотором участке, а ребра, связывающие эти вершины, - работы, которые возможно начать по совершении одного события и необходимо выполнить для совершения следующего.
Граф можно начертить «одним росчерком» тогда и только тогда, когда он содержит не более 2 нечетных вершин, причем маршрут начинается в одной из таких вершин и заканчивается в другой. Но, поскольку граф на этом рисунке имеет четыре нечетные вершины, то такой граф начертить «одним росчерком» невозможно.
Граф, который можно нарисовать, не отрывая карандаша от бумаги, называется эйлеровым.
Сфера применения графов
Примерами графов могут служить схемы авиалиний, дорог, электросхемы, чертежи многоугольников.
Решение задач с помощью графов
В некоторых задачах условие, записанное с помощью рисунка, помогает найти правильный ход решения.
Для этого воспользуемся алгоритмом.
Алгоритм составления графа.
1. О каком процессе идет речь? 2. Какие величины характеризуют данный процесс? 3. Каким соотношением связаны эти величины? 4.Сколько процессов описывается в задаче? 5.Есть ли связь между элементами?
Если ответы на эти вопросы записывать схематически, то эта схема и будет сетевым графом.
Я задумал число . Если к нему прибавить 24, потом полученную сумму умножить на 9, затем из произведения вычесть 76 и, наконец, полученную разность разделить на 19, то получится число 23. Найти задуманное число.
Решение : Сделаем рисунок.
Исходя из рисунка, видим, чтобы найти задуманное число, надо выполнить обратные действия:
Применение теории графов к решению задач
Графы существуют везде, и даже маленькие дети неожиданно сталкиваются с ними, когда рисуют или играют. Они встречаются на картах дорог, созвездий, при построении схем и чертежей. Графы лежат в основе многих компьютерных программ, которые делают возможными современную коммуникацию и технологические процессы.
Графы способствуют развитию мышления как логического, так и абстрактного.
При решении задач, наверное, не раз приходилось изображать объекты точками, соединять их отрезками или стрелками, при этом для решения задачи был использован специальный математический аппарат, а именно была применена теория графов.
Исторически сложилось так, что теория графов зародилась двести с лишним лет назад именно в ходе решения головоломок. Первая работа о графах появилась в 1736 году в публикациях Петербургской академии наук. Она принадлежит Леонарду Эйлеру и связана с решением задачи о кенигсбергских мостах. Вопрос заключался в том, можно ли совершить прогулку так, чтобы выйдя из дома, вернуться обратно, пройдя в точности по одному разу каждый из семи кенигсбергских мостов. (Слайд 2). Эту задачу можно представить в виде геометрической схемы, на которой точки изображают части суши, а линии, их соединяющие – мосты. (Слайд 3).
Схема такого вида называется графом. Точки – вершины графа, соединяющие их линии – ребра.
С теорией графов связаны также задачи на вычерчивание фигуры одним росчерком. Если степени всех вершин четные, то можно обойти все вершины графа без повторений, также можно обойти все вершины, если на графе только 2 нечетные вершины, если же нечетных вершин больше, то обойти все вершины графа не удастся.
В переводе на задачи “одним росчерком” это звучит так: “Если на рисунке все точки четные, то такой рисунок можно нарисовать одной линией, не отрывая карандаша от бумаги и не проводя дважды по одной линии; если на рисунке 2 нечетные точки (если есть одна нечетная точка, то обязательно есть и вторая), то такой рисунок также можно нарисовать одним росчерком, причем следует начинать с одной нечетной точки и заканчивать в другой нечетной точке; если же нечетных точек больше двух, то нарисовать такой рисунок одним росчерком не удастся.”
Так обвести одной линией рисунок (слайд 4) нельзя, т.к. он содержит сразу 8 нечетных точек.
Толчок же к развитию теория графов получила на рубеже XIX–XX столетий, когда резко выросло число работ в области топологии и комбинаторики, с которыми ее связывают самые тесные узы родства. Как отдельная математическая дисциплина теория графов была впервые представлена в 30 годы ХХ столетия.
Однако теория графов пока не нашла своего отражения в большинстве учебниках математики. Отличаясь простотой теоретических сведений, наглядностью и доступностью, теория графов может с пользой найти отражение на самом раннем этапе обучения школьников. С помощью этой теории можно решить на доступном для младших школьников уровне ряд достаточно сложных задач.
Граф представляет собой непустое множество точек и множество отрезков, оба конца которых принадлежат заданному множеству точек.
При изображении графов на рисунках или схемах отрезки могут быть прямолинейными и криволинейными; длины отрезков и расположение точек произвольны.
Как уже было сказано выше, точки, изображающие элементы множества, называются вершинами графа; отрезки – ребрами графа. Вершины графа на рисунке выделяют обычно кружками или квадратиками хотя бы потому, чтобы точки пересечения ребер не принимались за вершины графа. Обозначают вершины обычно заглавными буквами русского или латинского алфавитов и иногда числами.
Можно выделить (слайд 5)
- неориентированный граф;
- граф с цветными ребрами;
- ориентированный граф;
- граф-дерево или дерево возможностей .
Рассмотрим применение всех этих видов графов к решению задач.
Неориентированные графы. (Слайд 6). В них ребрами являются отрезки или части кривой линии.
Рассмотрим задачу: “В шахматном турнире участвовали 4 человека. Каждый спортсмен сыграл со всеми другими участниками соревнований по одному разу. Сколько всего было сыграно партий?” (Слайд 7). Изобразим участников турнира точками, а сыгранные ими партии – отрезками. (Слайд 8). Для того чтобы ответить на вопрос задачи, надо лишь подсчитать число проведенных отрезков, их 6, следовательно, было сыграно 6 партий.
Рассмотрим еще одну подобную задачу: “На лесной опушке встретились заяц, белка, лиса, волк, медведь и куница. Каждый, здороваясь, пожал каждому лапу. Сколько всего лапкопожатий было сделано? (Слайд 9). На графе 15 ребер, следовательно, было сделано 15 лапкопожатий. Для того чтобы упростить подсчет ребер графа, можно рассуждать так: из каждой из 6 точек выходит 5 отрезков, т.е. для подсчета отрезков умножаем 5 на 6, получаем 30, но при этом каждый отрезок мы посчитаем дважды (например, белка – лиса и лиса – белка). Следовательно, чтобы найти число ребер графа, надо 30 разделить на 2, получим.15. Такие рассуждения будут особенно полезны, когда граф содержит большее число вершин и подсчет числа ребер становится затруднительным.
Рассмотрим обратную задачу: “Несколько мальчиков встретились на вокзале, чтобы поехать за город в лес. При встрече все они поздоровались друг с другом за руку. Сколько мальчиков поехало за город, если всего было10 рукопожатий?” (Слайд 10).
Предположим, что встретились два мальчика, изобразим их точками, а рукопожатие линией, соединяющей эти точки. (Слайд 11). Добавляем третьего приятеля и получаем три рукопожатия. (Слайд 12). Значит, необходимо добавить еще четвертого мальчика. Если встретились четыре мальчика, то рукопожатий будет шесть. (Слайд 13). Необходимо добавить следующего, пятого мальчика. На получившемся графе видно (Слайд 14), что рукопожатий получилось 10. Следовательно, на вокзале встретилось пять мальчиков.
Рассмотрим еще один вид задач, где применимы неориентированные графы: “В первенстве класса по шашкам 5 участников: Аня, Боря, Влад, Гриша, Даша. Первенство проводится по круговой системе – каждый из участников играет с каждым из остальных один раз. К настоящему времени некоторые игры уже проведены: Аня сыграла с Борей, Владом и Дашей; Боря сыграл, как уже говорилось, с Аней и еще с Гришей; Влад – с Аней и Дашей, Гриша – с Борей, Даша – с Аней и Гришей. Сколько игр проведено к настоящему времени и сколько еще осталось?” (Слайд 15).
Участников соревнований изобразим точками, которые назовем первыми буквами имен детей. Если двое участников уже сыграли между собой, соединим изображающие их точки отрезками. Получим граф. (Слайд 16).
Число игр, проведенных к настоящему моменту, равно числу ребер, т.е. шести. Чтобы узнать число игр, которые осталось провести, соединим линиями другого цвета (или пунктиром) тех участников, которые еще не играли друг с другом. Таких ребер получилось 4, значит, осталось провести 4 игры: Борис – Влад, Борис – Даша, Влад – Гриша, Гриша – Аня. (Слайд 16).
Применить теорию графов можно и при решении следующей задачи: “В стране алфавит 8 городов: А, Б, В, Г, Д, Е, Ж, З и восемь непересекающихся дорог между городами А и Б, Е и Д, Б и Ж, З и А, В и Г, Г и Д, Ж и З, В и Е. Можно ли по этим дорогам проехать из А в Г?” (Слайд 17).
Построим по условию задачи граф, при этом все вершины графа сразу отмечать не будем. Начнем с построения ребер графа, учитывая то условие, что они не пересекаются. Построим отрезки АБ и ЕД, присоединим к отрезку АБ отрезки БЖ и ЗА. Построим отрезок ВГ, не пересекающий ни один из построенных отрезков и соединим точки Г и Д, Ж и З, В и Е (не обязательно отрезками, можно и кривыми линиями). По графу видно, что точки А и Г друг с другом не соединены, а значит, по указанным дорогам из города А в город Г проехать нельзя. (Слайд 18).
Для решении задач на упорядочивание множеств будем применять ориентированные графы. (Слайд 19). В этом случае одну вершину считают началом ребра, а другую – концом. В ориентированном графе все ребра должны быть ориентированы.
Рассмотрим задачу: “Из лагеря вышли четыре туриста: Вася, Галя, Толя и Лена. Вася идет впереди Лены, Толя впереди Гали, а Лена впереди Толи. В каком порядке идут дети?
Попробуем вначале эту задачу решить без использования графа. При этом условие, что Толя идет впереди Гали придется вначале пропустить, т.к. неясно, они идут перед Васей и Леной или позади их. И только после прочтения последнего условия и установления, что Толя идет за Леной, можно определить месторасположение Гали. (Слайд 20).
Когда же мы решаем эту задачу при помощи графов, нам лишь необходимо представить условие задачи на графе. Изобразим всех туристов точками, которые обозначим первыми буквами имен детей. В задаче рассматривается отношение “идти впереди”, поэтому стрелку будем ставить от впереди идущего к идущему вслед за ним. Вася идет впереди Лены, значит стрелку ставим от Васи к Лене. Толя впереди Гали – стрелку ставим от Толи к Гале. Также ставим стрелку от Лены к Толе, т.к. она идет впереди него. На графе видно (Слайд 21), что первый идет Вася, за ним Лена, Толя и Галя идет последней.
Рассмотрим еще одну задачу: “В детском лагере отдыха в одной комнате живут четыре девочки: Маша, Валя, Таня и Галя. Две из них ровесницы. Известно, что Таня старше Маши, которая моложе Гали. Таня моложе Вали, которая старше Гали. Кто ровесницы?” При решении задачи без использования графа будем расставлять первые буквы имен девочек от младшей к старшей. Из условия, что Маша моложе Гали непонятно, где поставить букву Г, слева или справа от буквы Т. И только после прочтения последнего условия можно сделать вывод, что Г стоит между Т и В. Получаем, что ровесниками могут быть только Таня и Валя. (Слайд 22).
Рассмотрим решение этой же задачи при помощи графа. В задаче рассматриваются два отношения “быть младше” и “быть старше”. Выберем одно из низ и построим граф отношения “быть старше”. При этом стрелку будем ставить от старшей девочки к младшей. (Слайд 23). По графу видно, что старше всех Валя, а Маша – младшая из девочек. Следовательно, ровесницы – это Галя и Таня.
Если такие простые задачи, в которых рассматривается множество, состоящее из небольшого числа элементов, еще можно решить без помощи графов, хотя такой способ решения является более сложным, то при решении задач на упорядочивание множества, состоящего из большого числа элементов, это становится практически невозможным.
Рассмотрим задачу: “На пришкольном участке растут 8 деревьев: яблоня, тополь, береза, рябина, дуб, клен, лиственница и сосна. Рябина выше лиственницы, яблоня выше клена, дуб ниже березы, но выше сосны, сосна выше рябины, береза ниже тополя, а лиственница выше яблони. Расположите деревья от самого низкого к самому высокому”. (Слайд 24). Будем решать ее при помощи графа. Для этого отметим все деревья точками, а точки обозначим первыми буквами названия деревьев. В задаче рассматриваются два отношения: “быть ниже” и “быть выше”. В нашем случае удобнее рассматривать отношение “быть ниже” и вести стрелку от более низкого дерева к более высокому. Если в задаче сказано, что рябина выше лиственницы, то стрелку ставим от лиственницы к рябине и т.д. Получаем граф, на котором видно, что самое низкое дерево – клен, затем идут яблоня, лиственница, рябина, сосна, дуб, береза и тополь. (Слайд 25).
Следующий тип графов, которые можно использовать при решении задач в начальной школе – это граф-дерево или дерево возможностей. Графы такого вида используются при решении комбинаторных задач, когда надо осуществить перебор всех возможных вариантов. (Слайд 26).
Рассмотрим задачу: “В столовой на горячее можно заказать щуку, грибы и баранину, на гарнир – картофель и рис, а из напитков – чай и кофе. Сколько различных вариантов обедов можно составить из указанных блюд? (Слайд 27).
Т.к. горячих блюд три, то поставим три точки. Каждую точку обозначим первой буквой названия блюда. От этих точек проведем по две линии вниз и поставим точки, т.к. гарниров два. Их также обозначим первыми буквами названий. От каждого гарнира также проведем по две линии, точки будут обозначать напиток. Каждый путь по этому графу соответствует одному из способов выбора. Число таких путей будет соответствовать числу точек в нижнем ряду. Сосчитаем точки третьего ряда на нашем графе. Их 12, значит, можно составить 12 различных обедов. (Слайд 28).
Рассмотрим еще одну, более сложную задачу: “Из наборного полотна взяли 2 карточки с цифрой 1 и 3 карточки с цифрой 5. Сколько различных пятизначных чисел можно составить из этих карточек?” (Слайд 29).
По графу видно, что всего таких чисел можно составить 10, причем все их можно легко перечислить. (Слайд 30).
Последний вид графов, которые мы рассмотрим – это граф с ребрами двух цветов. (Слайд 31). Эти графы соответствуют таким ситуациям, в которых одни пары элементов множества находятся между собой в данном отношении, а другие – нет.
Рассмотрим задачу: “В одном классе учатся Иван, Петр и Сергей. Их фамилии Иванов, Петров и Сергеев. Установи фамилию каждого из ребят, если известно, что Иван не Иванов, Петр не Петров и Сергей не Сергеев и что Сергей живет в одном доме Петровым”. (Слайд 32).
В этой задаче речь идет о двух множествах: множестве имен и множестве фамилий. В этом случае, конечно, можно решить задачу с использованием таблицы, но для решения задач с тремя множествами таблицы уже будут непригодны. В этом случае решение задачи можно осуществить с помощью графов. Обозначим имена мальчиков точками, точно также поступим и с множеством фамилий. Если для данной пары элементов отношение выполняется, то соединим их красной линией, а если нет – черной. (Слайд 33). На графе видно, что Иван не Иванов, Петр – не Петров, Сергей – не Сергеев и не Петров, т.к. Сергей и Петров живут в одном доме. Поскольку Сергей – не Сергеев и не Петров, то, значит, он Иванов. Проведем красную линию от Сергея к Иванову. Тогда Ивановым Петр быть не может – соединим соответствующие точки черной линией. Итак, Петр – не Иванов и не Петров, следовательно, он Сергеев. Остается, что Иван носит фамилию Петров.
Рассмотрим задачу, в которой требуется установить соответствие между тремя множествами: “Три друга – Алеша, Сергей и Денис – купили щенков разной породы: щенка ротвейлера, щенка колли и щенка овчарки. Известно, что: щенок Алеши темнее по окрасу, чем ротвейлер, Леси и Гриф; щенок Сергея старше Грифа, ротвейлера и овчарки; Джек и ротвейлер всегда гуляют вместе. У кого какой породы щенок? Назовите клички щенков.” (Слайд 34).
Изобразим условие задачи при помощи графа. (Слайды 35–37). В результате получим, что у Сергея щенок породы колли Леси, у Алеши щенок овчарки Джек, у Дениса щенок ротвейлера по кличке Гриф.
Рассмотренные выше задания составляют большую часть решаемых с помощью графов задач, доступных по уровню сложности младшим школьникам.
Логические задачи для 6 класса
методическая разработка по информатике и икт (6 класс) по теме
Задания для самостоятельной работы в 6 классе по программе Босовой Л.Л. по теме "Умозаключение как форма мышления".
| Вложение | Размер |
|---|---|
| logicheskie_zadachi.docx | 33.87 КБ |
Буклет "Еще один увлекательный способ решения задач ( метод графов)"
методическая разработка по алгебре (6 класс) на тему
Данный буклет представляет собой справочный материал по применению графов для решения задач.
| Вложение | Размер |
|---|---|
| buklet_grafy.docx | 163.2 КБ |
Читайте также: